Question

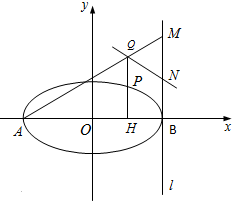如图，已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的长轴为AB，点（0，1）恰好是椭圆的一个顶点，且椭圆的离心率e=

3

2

，
过点B的直线l与x轴垂直．
（1）求椭圆的标准方程；
（2）设P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，
延长HP到点Q使得HP=PQ，连结AQ延长交直线l于点M，N为MB的中点．
①求点Q的轨迹；
②判断直线QN与以AB为直径的圆O的位置关系．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由点（0，1）是椭圆的一个顶点，且椭圆的离心率e=

3

2

，k可得

b=1 3 2 = 1- b2 a2

，解出即可．
（2））①设P（x₀，y₀），Q（x，y）．由HP=PQ，利用中点坐标公式可得

x0=x y0= 1 2 y

，代入椭圆方程即可得出；
②又A（-2，0），可得直线AQ的方程为y=

2y0

x0+2

(x+2)．令x=2，得M(2，

8y0

x0+2

)．又B（2，0），N为MB的中点，可得N(2，

4y0

x0+2

)．计算

OQ

•

NQ

即可得出．

解答： 解：（1）由点（0，1）是椭圆的一个顶点，且椭圆的离心率e=

3

2

，
∴

b=1 3 2 = 1- b2 a2

，解得b=1，a²=4．
∴椭圆的标准方程为

x2

4

+y2=1．
（2）①设P（x₀，y₀），Q（x，y）．
∵HP=PQ，∴

x=x0 y=2y0

．
∴

x0=x y0= 1 2 y

∵

x02

4

+y02=1，
∴

x2

4

+

y2

4

=1，即x²+y²=4．
∴Q点在以O为圆心，2为半径的圆上．即Q点在以AB为直径的圆O上．
②又A（-2，0），
∴直线AQ的方程为y=

2y0

x0+2

(x+2)．
令x=2，得M(2，

8y0

x0+2

)．
又B（2，0），N为MB的中点，
∴N(2，

4y0

x0+2

)．
∴

OQ

=(x0，2y0)，

NQ

=(x0-2，

2x0y0

x0+2

)．
∴

OQ

•

NQ

=x₀（x₀-2）+

4x0 y 2 0

x0+2

=x0(x0-2)+

x0(4- x 2 0 )

x0+2

=x₀（x₀-2）+x₀（2-x₀）=0．
∴

OQ

⊥

NQ

．
∴直线QN与圆O相切．

点评：本题考查了椭圆的标准方程及其性质、圆的方程、直线与圆的位置关系、中点坐标公式、向量垂直与数量积的关系，考查了推理能力与计算能力，属于难题．