题目内容
直线经过点A（3，4），斜率为-
，则其方程为（ ）
| 3 |
| 4 |
| A、3x+4y-25=0 |
| B、3x+4y+25=0 |
| C、3x-4y+7=0 |
| D、4x+3y-24=0 |
考点：直线的点斜式方程
专题：直线与圆
分析：利用点斜式即可得出．
解答：
解：由点斜式可得：y-4=-
（x-3），
化为3x+4y-25=0．
故选：A．
| 3 |
| 4 |
化为3x+4y-25=0．
故选：A．
点评：本题考查了直线的点斜式方程，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某小组共有10名学生，其中女生3名，现选举2名代表，至少有1名女生当选的不同选法共（ ）种．
| A、27 | B、48 | C、21 | D、24 |
F1，F2是椭圆C：
+
=1（a＞b＞0）的左右焦点，过F1的直线l与C交于A，B两点，若|AB|=5，|BF2|=7，|AF2|=8，则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数在x=0处连续的是（ ）
A、f （x ）=
| ||||||
| B、f （x ）=lnx | ||||||
C、f （x ）=
| ||||||
D、f （x ）=
|
若A是△ABC的内角，当cosA=
，则cos
=（ ）
| 7 |
| 25 |
| A |
| 2 |
A、±
| ||
B、
| ||
C、±
| ||
D、
|
已知A，B，C为三角形的三个内角，它们的对边长分别为a，b，c，已知直线xsinA+ysinB+sinC=0到原点的距离大于1，则此三角形为（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
等差数列{an}中，前n项Sn=
n2+
n，则a3的值为（ ）
| 1 |
| 2 |
| a3 |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
随机变量x的分布列P（x=k）=
（k=1，2，3，4），其中P为常数，则P（
＜x＜
）=（ ）
| P |
| k(k+1) |
| 1 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
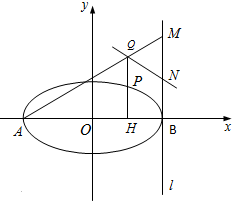如图，已知椭圆