题目内容
已知等比数列{an}的首项为a1=2,前n项和为Sn,且a2是3a2+2与-3的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn.
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:(1)利用等差数列与等比数列的通项公式即可得出.
(2)利用等比数列的前n项和公式即可得出.
(2)利用等比数列的前n项和公式即可得出.
解答:
解(1)设 等比数列{an}的公比为q,
∵a2是3a2+2与-3的等差中项.
∴2a2=3a2+2-3.
又a1=2,
∴4q=6q+2-3,解得q=
.
∴an=a1qn-1=
.
(2)Sn=
=4(1-
).
∵a2是3a2+2与-3的等差中项.
∴2a2=3a2+2-3.
又a1=2,
∴4q=6q+2-3,解得q=
| 1 |
| 2 |
∴an=a1qn-1=
| 1 |
| 2n-2 |
(2)Sn=
2(1-
| ||
1-
|
| 1 |
| 2n |
点评:本题考查了等差数列与等比数列的通项公式及其等比数列的前n项和公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
随机变量x的分布列P(x=k)=
(k=1,2,3,4),其中P为常数,则P(
<x<
)=( )
| P |
| k(k+1) |
| 1 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
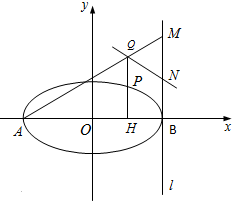 如图,已知椭圆
如图,已知椭圆 某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示: 某海轮以30n mile/h的速度航行,在A点测得海面上油井P在南偏东60°方向,向北航行40min后到达B点,测得油井P在南偏东30°方向,海轮改为北偏东60°的航向再行驶80min到达C点,求P、C间的距离.
某海轮以30n mile/h的速度航行,在A点测得海面上油井P在南偏东60°方向,向北航行40min后到达B点,测得油井P在南偏东30°方向,海轮改为北偏东60°的航向再行驶80min到达C点,求P、C间的距离.