题目内容
已知y=x2-|x|+a与y=2有4个不同的交点，求a的取值范围．
考点：函数的图象
专题：函数的性质及应用
分析：在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a的图象，观察求解．
解答：
解：如图，在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a=
观图可知，a的取值必须满足
，解得2＜a＜
，
故a的取值范围为（2，
）
解：如图，在同一直角坐标系内画出直线y=2与曲线y=x2-|x|+a=
|
观图可知，a的取值必须满足
|
| 9 |
| 4 |
故a的取值范围为（2，
| 9 |
| 4 |
点评：本题主要考查了绝对值函数的图象的画法，关键是化为分段函数，属于基础题，
练习册系列答案
相关题目
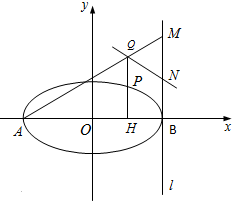如图，已知椭圆
某校从高一年级期末考试的学生中抽出60名学生，其成绩（均为整数）的频率分布直方图如图所示：
某海轮以30n mile/h的速度航行，在A点测得海面上油井P在南偏东60°方向，向北航行40min后到达B点，测得油井P在南偏东30°方向，海轮改为北偏东60°的航向再行驶80min到达C点，求P、C间的距离．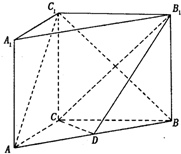
如图，AA1∥BB1∥CC1，AA1=BB1=CC1，AA1⊥面ABC且AC=3，BC=4，AB=5，AA1=4，点D为 AB的中点．
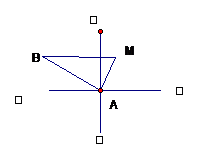一艘轮船按照北偏西50°的方向，以15海里每小时的速度航行，一个灯塔M原来在轮船的北偏东10°方向上，经过40分钟，轮船与灯塔的距离是5