题目内容
若非空集合A={x|a-3≤x≤4a-12}，B={x|-2≤x≤12}，则能使A∩B=A，成立的实数a的集合是（ ）
| A、{a|3≤a≤6} |
| B、{a|1≤a≤6} |
| C、{a|a≤6} |
| D、∅ |
考点：交集及其运算
专题：集合
分析：由A与B的交集为A，且A不为空集，求出a的范围即可．
解答：
解：∵非空集合A={x|a-3≤x≤4a-12}，B={x|-2≤x≤12}，且A∩B=A，
∴
，且a-3≤4a-12，
解得：3≤a≤6，
则a的范围为{a|3≤a≤6}．
故选：A．
∴
|
解得：3≤a≤6，
则a的范围为{a|3≤a≤6}．
故选：A．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
F1，F2是椭圆C：
+
=1（a＞b＞0）的左右焦点，过F1的直线l与C交于A，B两点，若|AB|=5，|BF2|=7，|AF2|=8，则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列{an}中，前n项Sn=
n2+
n，则a3的值为（ ）
| 1 |
| 2 |
| a3 |
| 2 |
| A、3 | B、4 | C、5 | D、6 |
随机变量x的分布列P（x=k）=
（k=1，2，3，4），其中P为常数，则P（
＜x＜
）=（ ）
| P |
| k(k+1) |
| 1 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
袋中有5个球，3个白球，2个黑球，现每次取一个，无放回地抽取两次，第二次抽到白球的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
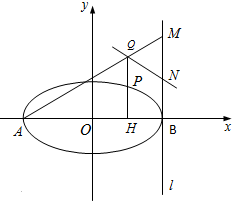如图，已知椭圆
某校从高一年级期末考试的学生中抽出60名学生，其成绩（均为整数）的频率分布直方图如图所示：