题目内容
已知式子(2x2+
)5.
(Ⅰ)求展开式中含
的项;
(Ⅱ)若(2x2+
)5的展开式中各二项式系数的和比(
+
)n的展开式中的第三项的系数少28,求n的值.
| 1 |
| x |
(Ⅰ)求展开式中含
| 1 |
| x2 |
(Ⅱ)若(2x2+
| 1 |
| x |
| x |
| 2 |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:(Ⅰ)在式子(2x2+
)5的通项公式中,令x的幂指数等于-2,求得r的值,可得展开式中含
的项.
(Ⅱ)先求得(
+
)n的展开式中的第三项,结合题意可得题意可得25=
×4-28,由此求得n的值.
| 1 |
| x |
| 1 |
| x2 |
(Ⅱ)先求得(
| x |
| 2 |
| x |
| C | 2 n |
解答:
解:(Ⅰ)式子(2x2+
)5的通项公式为 Tr+1=
•25-r•x10-3r,
令10-3r=-2,求得r=4,故展开式中含
的项为 T5=
×2×
=
.
(Ⅱ)(
+
)n的展开式中的第三项为 T3=
•4•x
-3,
由题意可得,25=
×4-28,解得
=15,∴n=6.
| 1 |
| x |
| C | r 5 |
令10-3r=-2,求得r=4,故展开式中含
| 1 |
| x2 |
| C | 4 5 |
| 1 |
| x2 |
| 10 |
| x2 |
(Ⅱ)(
| x |
| 2 |
| x |
| C | 2 n |
| n |
| 2 |
由题意可得,25=
| C | 2 n |
| C | 2 n |
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=2x2-lnx的递减区间是( )
A、(0,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-∞,-
|
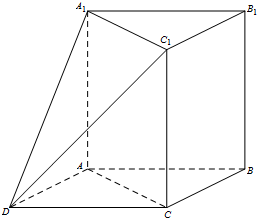 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1. 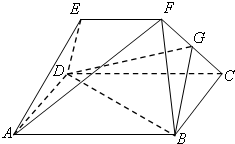 如图几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF∥AB,AF⊥CF.
如图几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF∥AB,AF⊥CF.