题目内容
已知x1、x2是函数f（x）=
-3的两个零点，若a＜x1＜x2，则f（a）的值满足 ．
| ex |
| x |
考点：函数零点的判定定理
专题：计算题,函数的性质及应用
分析：将函数的零点问题转化为求两个函数的交点问题，通过图象读出g（a），h（a）的大小，从而解决问题．
解答：
解：令f（x）=0，∴ex=3x，
令g（x）=ex，h（x）=3x，
如图示：
由图象可得：x＜x1时，ex＞3x，
∴f（a）=
，
∵ea-3a＞0，
∴a＞0时：f（a）＞0；
当a＜0时：ea-3a＞0，a＜0，
∴f（a）＜0，
故答案为：符号不确定．
解：令f（x）=0，∴ex=3x，令g（x）=ex，h（x）=3x，
如图示：
由图象可得：x＜x1时，ex＞3x，
∴f（a）=
| ea-3a |
| a |
∵ea-3a＞0，
∴a＞0时：f（a）＞0；
当a＜0时：ea-3a＞0，a＜0，
∴f（a）＜0，
故答案为：符号不确定．
点评：本题考查了函数的零点问题，渗透了转化思想，数形结合思想，是一道中档题．
练习册系列答案
口算能手系列答案
相关题目
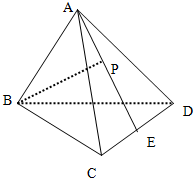已知空间四边形ABCD，BC=BD，AC=AD，E是CD边的中点．在AE上的一个动点P，讨论BP与CD是否存在垂直关系，并证明你的结论．
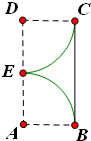如图，在矩形ABCD中，E为边AD的中点，AB=1，BC=2，分别以A，D为圆心，1为半径作圆弧EB，EC，若由两圆弧EB，EC及边BC所围成的平面图形绕直线AD旋转一周，则所形成的几何体的表面积为