题目内容
2.已知圆O:x2+y2=5和点A(2,1)则过点A且和圆O相切的直线与两坐标轴围成的三角形的面积等于$\frac{25}{4}$.分析 判断点A在圆上,用点斜式写出切线方程,求出切线在坐标轴上的截距,从而求出直线与两坐标轴围成的三角形的面积.
解答 解:由题意知,点A在圆上,则A为切点,
∴OA的斜率k=$\frac{1}{2}$,
∴切线斜率为-2,
则切线方程为:y-1=-2(x-2),
即2x+y-5=0,从而求出在两坐标轴上的截距分别是5和$\frac{5}{2}$,
∴所求面积S=$\frac{1}{2}×5×\frac{5}{2}$=$\frac{25}{4}$.
故答案为:$\frac{25}{4}$.
点评 本题考查求圆的切线方程的方法,以及求直线与坐标轴围成的三角形的面积.判断A是切点是解决本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
12.当x,y满足条件$\left\{\begin{array}{l}{x≥y}\\{y≥0}\\{2x+y-3≥0}\end{array}\right.$时,目标函数z=x+3y的最小值是( )
| A. | 0 | B. | 1.5 | C. | 4 | D. | 9 |
13.已知{an}是等比数列,给出以下四个命题:①{2a3n-1}是等比数列;②{an+an+1}是等比数列;③{anan+1}是等比数列;④{lg|an|}是等比数列,下列命题中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.$若log_a^{\;}\frac{2}{3}<1,(a>0且a≠1)$,则a的取值范围是( )
| A. | ($\frac{2}{3}$,1) | B. | (0,$\frac{2}{3}$)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) |
7.下列条件能唯一确定一个平面的是( )
| A. | 空间任意三点 | B. | 不共线三点 | C. | 共线三点 | D. | 两条异面直线 |
12.如表示采集的商品零售额(万元)与商品流通费率的一组数据:
(1)将商品零售额作为横坐标,商品流通费率作为纵坐标,在平面直角坐标系内作出散点图;
(2)商品零售额与商品流通费率具有线性相关关系吗?如果商品零售额是20万元,那么能否预测此时流通费率是多少呢?(b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$ a=$\overline{y}$-b$\overline{x}$)
| 商品零售额 | 9.5 | 11.5 | 13.5 | 15.5 | 17.5 | 19.5 | 21.5 | 23.5 | 25.5 | 27.5 |
| 商品流通费率 | 6.0 | 4.6 | 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 2.2 | 2.1 |
(2)商品零售额与商品流通费率具有线性相关关系吗?如果商品零售额是20万元,那么能否预测此时流通费率是多少呢?(b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$ a=$\overline{y}$-b$\overline{x}$)
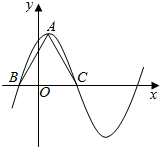 函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象
函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象