题目内容
12．当x，y满足条件$\left\{\begin{array}{l}{x≥y}\\{y≥0}\\{2x+y-3≥0}\end{array}\right.$时，目标函数z=x+3y的最小值是（ ）| A． | 0 | B． | 1.5 | C． | 4 | D． | 9 |
分析 作$\left\{\begin{array}{l}{x≥y}\\{y≥0}\\{2x+y-3≥0}\end{array}\right.$表示的平面区域，而化简z=x+3y=-$\frac{1}{3}$x+$\frac{1}{3}$z，$\frac{1}{3}$z是直线的截距，从而解得．
解答 
解：作$\left\{\begin{array}{l}{x≥y}\\{y≥0}\\{2x+y-3≥0}\end{array}\right.$表示的平面区域如下，
，化简z=x+3y=-$\frac{1}{3}$x+$\frac{1}{3}$z，$\frac{1}{3}$z是直线的截距，
故目标函数z=x+3y的最小值在A（1.5，0）上取得，
故z=1.5；
故选B．
点评 本题考查了线性规划的解法及数形结合的思想应用，注意利用斜截式．
练习册系列答案
相关题目
3．
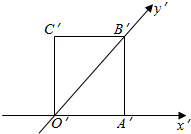如图的正方形O′A′B′C′的边长为1cm，它是水平放置的一个平面图形的直观图，则原图形的面积为（ ）
如图的正方形O′A′B′C′的边长为1cm，它是水平放置的一个平面图形的直观图，则原图形的面积为（ ）| A． | 2$\sqrt{2}$cm2 | B． | 1cm2 | C． | 4$\sqrt{2}$cm2 | D． | $\frac{\sqrt{2}}{4}$cm2 |
7．对于集合A、B，“A≠B”是“A∩B?A∪B”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分也非必要条件 |