题目内容
13．已知{an}是等比数列，给出以下四个命题：①{2a3n-1}是等比数列；②{an+an+1}是等比数列；③{anan+1}是等比数列；④{lg|an|}是等比数列，下列命题中正确的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据等比数列的判断方法，分别检验比值是否为常数进行判断．
解答 解：{an}是等比数列可得$\frac{{a}_{n}}{{a}_{n-1}}$=q（q是定值）
①$\frac{2{a}_{3n-1}}{2{a}_{3n-4}}$=q3是定值，故①正确；
②比如an=（-1）n，故②不正确；
③$\frac{{a}_{n}{a}_{n+1}}{{a}_{n-1}{a}_{n}}$=q2是定值，故③正确；
④$\frac{lg|{a}_{n}|}{lg|{a}_{n-1}|}$不一定为常数，故④错误．
故选B．
点评 要判断一个数列是否是等比数列常用的方法，可以利用等比数列的定义只需判断数列的任意一项与它的前一项的比是否是常数．
练习册系列答案
相关题目
3．
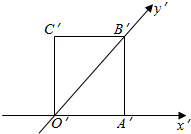如图的正方形O′A′B′C′的边长为1cm，它是水平放置的一个平面图形的直观图，则原图形的面积为（ ）
如图的正方形O′A′B′C′的边长为1cm，它是水平放置的一个平面图形的直观图，则原图形的面积为（ ）| A． | 2$\sqrt{2}$cm2 | B． | 1cm2 | C． | 4$\sqrt{2}$cm2 | D． | $\frac{\sqrt{2}}{4}$cm2 |
8．一个弹性小球从10米自由落下，着地后反弹到原来高度的$\frac{4}{5}$处，再自由落下，又弹回到上一次高度的$\frac{4}{5}$处，假设这个小球能无限次反弹，则这个小球在这次运动中所经过的总路程为（ ）
| A． | 50 | B． | 80 | C． | 90 | D． | 100 |
18．在一个有穷数列每相邻两项之间添加一项，使其等于两相邻项的和，我们把这样的操作叫做该数列的一次“H扩展”．已知数列1，2．第一次“H扩展”后得到1，3，2；第二次“H扩展”后得到1，4，3，5，2； 那么第10次“H扩展”后得到的数列的所有项的和为（ ）
| A． | 88572 | B． | 88575 | C． | 29523 | D． | 29526 |
5．已知$\overrightarrow a$，$\overrightarrow b$是单位向量，$\overrightarrow a•\overrightarrow b=0$，且向量$\overrightarrow c$满足$|\overrightarrow c-\overrightarrow a-\overrightarrow b|$=1，则|$\overrightarrow c$|的取值范围是（ ）
| A． | $[\sqrt{2}-1，\;\sqrt{2}+1]$ | B． | $[\sqrt{2}-1，\;\sqrt{2}]$ | C． | $[\sqrt{2}，\;\sqrt{2}+1]$ | D． | $[2-\sqrt{2}，\;2+\sqrt{2}]$ |