题目内容
17.$若log_a^{\;}\frac{2}{3}<1,(a>0且a≠1)$,则a的取值范围是( )| A. | ($\frac{2}{3}$,1) | B. | (0,$\frac{2}{3}$)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) |
分析 把1变成底数的对数,讨论底数与1的关系,确定函数的单调性,根据函数的单调性整理出关于a的不等式,得到结果,把两种情况求并集得到结果.
解答 解:∵loga$\frac{2}{3}$<1=logaa,
当a>1时,函数是一个增函数,不等式成立,
当0<a<1时,函数是一个减函数,根据函数的单调性有a<$\frac{2}{3}$,
综上可知a的取值是(0,$\frac{2}{3}$)∪(1,+∞),
故选:B.
点评 本题主要考查对数函数单调性的应用、不等式的解法等基础知识,本题解题的关键是对于底数与1的关系,这里应用分类讨论思想来解题.

练习册系列答案
相关题目
7.对于集合A、B,“A≠B”是“A∩B?A∪B”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
8.一个弹性小球从10米自由落下,着地后反弹到原来高度的$\frac{4}{5}$处,再自由落下,又弹回到上一次高度的$\frac{4}{5}$处,假设这个小球能无限次反弹,则这个小球在这次运动中所经过的总路程为( )
| A. | 50 | B. | 80 | C. | 90 | D. | 100 |
5.已知$\overrightarrow a$,$\overrightarrow b$是单位向量,$\overrightarrow a•\overrightarrow b=0$,且向量$\overrightarrow c$满足$|\overrightarrow c-\overrightarrow a-\overrightarrow b|$=1,则|$\overrightarrow c$|的取值范围是( )
| A. | $[\sqrt{2}-1,\;\sqrt{2}+1]$ | B. | $[\sqrt{2}-1,\;\sqrt{2}]$ | C. | $[\sqrt{2},\;\sqrt{2}+1]$ | D. | $[2-\sqrt{2},\;2+\sqrt{2}]$ |
9.直线4x-3y=0与圆x2+y2=36的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不能确定 |
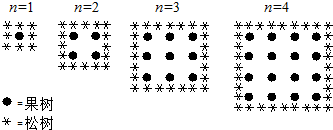 某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在如图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:
某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在如图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律: