题目内容
如果x>0,y>0,且2x+y=2,则
+
的最小值是( )
| 2 |
| x |
| 2 |
| y |
| A、4 | ||
| B、3 | ||
C、2
| ||
D、3+2
|
考点:基本不等式
专题:不等式的解法及应用
分析:利用“乘1法”和基本不等式即可得出.
解答:
解:∵x>0,y>0,且2x+y=2,
∴
+
=
(2x+y)×2(
+
)=(2x+y)(
+
)=3+
+
≥3+2
=3+2
,当且仅当x=
y=
时取等号.
因此
+
的最小值是3+2
.
故选;D.
∴
| 2 |
| x |
| 2 |
| y |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| 2x |
| y |
| y |
| x |
|
| 2 |
| 2 |
8-2
| ||
| 7 |
因此
| 2 |
| x |
| 2 |
| y |
| 2 |
故选;D.
点评:本题考查了“乘1法”和基本不等式,属于基础题.

练习册系列答案
相关题目
有一段演绎推理:“因为对数函数y=logax是减函数;已知y=log2x是对数函数,所以y=log2x是减函数”,结论显然是错误的,这是因为( )
| A、推理形式错误 |
| B、小前提错误 |
| C、大前提错误 |
| D、非以上错误 |
已知数列{an}满足an+an+1=
(n∈N*),其中a1=-
,试通过计算a2,a3,a4,a5,猜想an等于( )
| (-1)n+1 |
| 2 |
| 1 |
| 2 |
A、an=
| |||||||||
B、an=-
| |||||||||
C、an=
| |||||||||
D、
|
不等式(x-3)(x-1)<0的解集是( )
| A、{x|1<x<3} |
| B、{x|x<1或x>3} |
| C、{x|x<1} |
| D、{x|x>3} |
为了得到函数y=sin(
x-
)的图象,只需将y=sin
x图象上的每个点纵坐标不变,横坐标( )
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知实数x,y满足
,则目标函数z=x+2y的最大值为( )
|
| A、1 | ||
B、
| ||
| C、4 | ||
| D、5 |
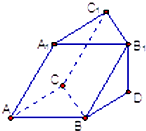 已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )
已知三棱柱ABC-A1B1C1的侧棱BB1在下底面的射影BD与AC平行,若BB1与底面所成角为30°,且∠B1BC=60°,则∠ACB的余弦值为( )