题目内容
已知函数f(x)=x•sinx,有下列四个结论:
①函数f(x)的图象关于y轴对称;
②存在常数T>0,对任意的实数x,恒有f(x+T)=f(x)成立;
③对于任意给定的正数M,都存在实数x0,使得|f(x0)|≥M;
④函数f(x)的图象上至少存在三个点,使得该函数在这些点处的切线重合.
其中正确结论的序号是 (请把所有正确结论的序号都填上).
①函数f(x)的图象关于y轴对称;
②存在常数T>0,对任意的实数x,恒有f(x+T)=f(x)成立;
③对于任意给定的正数M,都存在实数x0,使得|f(x0)|≥M;
④函数f(x)的图象上至少存在三个点,使得该函数在这些点处的切线重合.
其中正确结论的序号是
考点:函数的图象
专题:函数的性质及应用
分析:①研究函数的奇偶性,可用偶函数的定义来证明之;
②研究的是函数的周期性,采用举对立面的形式说明其不成立;
③找出一个常数M,都存在实数x0,使得|f(x0)|≥M成立即可;
④根据切线的几何意义,先求导,在找到特殊点,求出切线方程即可.
②研究的是函数的周期性,采用举对立面的形式说明其不成立;
③找出一个常数M,都存在实数x0,使得|f(x0)|≥M成立即可;
④根据切线的几何意义,先求导,在找到特殊点,求出切线方程即可.
解答:
 解:对于①,∵f(-x)=-x•sin(-x)=xsinx=f(x),
解:对于①,∵f(-x)=-x•sin(-x)=xsinx=f(x),
∴函数为偶函数,∴函数f(x)的图象关于y轴对称,故①正确;
对于②∵当x=2kπ+
时,f(x)=x,随着x的增大函数值也在增大,所以不会是周期函数,故②错;
对于③取M=1,当x0=
时,|f(
)|=
≥1;故③正确;
对于④∵f′(x)=sinx+xcosx,
当x=2kπ+
,f′(2kπ+
)=1=k,
f(2kπ+
)=2kπ+
∴切线方程为y-2kπ-
=x-2kπ-
即切线方程为y=x,
∴函数f(x)的图象上至少存在三个点,使得该函数在这些点处的切线重合,故④正确
(为了让学生更加理解,特画图)
故答案为:①③④
 解:对于①,∵f(-x)=-x•sin(-x)=xsinx=f(x),
解:对于①,∵f(-x)=-x•sin(-x)=xsinx=f(x),∴函数为偶函数,∴函数f(x)的图象关于y轴对称,故①正确;
对于②∵当x=2kπ+
| π |
| 2 |
对于③取M=1,当x0=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
对于④∵f′(x)=sinx+xcosx,
当x=2kπ+
| π |
| 2 |
| π |
| 2 |
f(2kπ+
| π |
| 2 |
| π |
| 2 |
∴切线方程为y-2kπ-
| π |
| 2 |
| π |
| 2 |
即切线方程为y=x,
∴函数f(x)的图象上至少存在三个点,使得该函数在这些点处的切线重合,故④正确
(为了让学生更加理解,特画图)
故答案为:①③④
点评:本题考点是函数的单调性判断与证明,函数的奇偶性,函数的中心对称的判断及函数的周期性,涉及到的性质比较多,且都是定义型,本题知识性较强,做题时要注意准确运用相应的知识准确解题.

练习册系列答案
相关题目
若-
<α<-
,从单位圆中的三角函数线观察sinα,cosα,tanα的大小是( )
| 3π |
| 4 |
| π |
| 2 |
| A、sinα<tanα<cosα |
| B、cosα<sinα<tanα |
| C、sinα<coasα<tanα |
| D、tanα<sinα<cosα |
已知直线a∥平面α,直线a⊥平面β,则( )
| A、α⊥β | B、α∥β |
| C、α与β不垂直 | D、以上都有可能 |
 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的体积为
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的体积为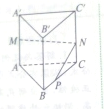 如图,在直棱柱ABC-A′B′C′中,底面是边长为3的等边三角形,AA′=4,M为AA′的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC′到M的最短路线长为
如图,在直棱柱ABC-A′B′C′中,底面是边长为3的等边三角形,AA′=4,M为AA′的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC′到M的最短路线长为