题目内容
已知sinα=m(|m|<1),求tanα,cosα
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由sinα,分象限,利用同角三角函数间的基本关系求出cosα的值,进而求出tanα的值即可.
解答:
解:∵sinα=m(|m|<1),
∴当α为第一象限,0<m<1时,cosα=
,tanα=
;
当α为第二象限,0<m<1时,cosα=-
,tanα=-
;
当α为第三象限,-1<m<0时,cosα=-
,tanα=-
;
当α为第四象限,-1<m<0时,cosα=
,tanα=
.
∴当α为第一象限,0<m<1时,cosα=
| 1-m2 |
| m | ||
|
当α为第二象限,0<m<1时,cosα=-
| 1-m2 |
| m | ||
|
当α为第三象限,-1<m<0时,cosα=-
| 1-m2 |
| m | ||
|
当α为第四象限,-1<m<0时,cosα=
| 1-m2 |
| m | ||
|
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
设集合A=[0,1),B=[1,2],函数f(x)=
,x0∈A,且f[f(x0)]∈A,则x0 的取值范围是( )
|
A、(
| ||
B、[0,
| ||
C、(log2
| ||
| D、(log32,1) |
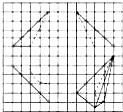 如图,网格纸上小正方形的边长为1,粗线或粗虚线画出了某简单组合体的三视图和直观图(斜二测画法),则此简单几何体的体积是
如图,网格纸上小正方形的边长为1,粗线或粗虚线画出了某简单组合体的三视图和直观图(斜二测画法),则此简单几何体的体积是