题目内容
若
＜α＜
，0＜β＜
且sin（α+
）=
，cos（
+β）=
，求sin（α+β）的值．
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| 5 |
| 13 |
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：首先，根据sin（α+
）=
，cos（
+β）=
，求解cos（α+
），sin（
+β），然后，结合诱导公式进行求值．
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| 5 |
| 13 |
| π |
| 4 |
| π |
| 4 |
解答：
解：∵
＜α＜
，
∴
＜α+
＜π，
∴cos(α+
)=-
=-
，
又∵0＜β＜
，
∴
＜β+
＜
，
∴sin(β+
)=
=
，
又∵-sin(α+β)=cos(α+β+
)=cos[(α+
)+(β+
)]
=cos(α+
)cos(β+
)-sin(α+
)sin(β+
)
=(-
)×
-
×
=-
，
∴sin（α+β）=
．
| π |
| 4 |
| 3π |
| 4 |
∴
| π |
| 2 |
| π |
| 4 |
∴cos(α+
| π |
| 4 |
1-sin2(α+
|
| 4 |
| 5 |
又∵0＜β＜
| π |
| 4 |
∴
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴sin(β+
| π |
| 4 |
1-cos2(α+
|
| 12 |
| 13 |
又∵-sin(α+β)=cos(α+β+
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
=cos(α+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=(-
| 4 |
| 5 |
| 5 |
| 13 |
| 12 |
| 13 |
| 3 |
| 5 |
| 56 |
| 65 |
∴sin（α+β）=
| 56 |
| 65 |
点评：本题重点考查了三角函数的求值、三角恒等变换公式等知识，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设a＞b＞0，a+b=1且x=（
）b，y=log (
+
)a，z=log
a，则x，y，z的大小关系是（ ）
| 1 |
| a |
| 1 |
| a |
| 1 |
| b |
| 1 |
| b |
| A、y＜x＜z |
| B、z＜y＜x |
| C、y＜z＜x |
| D、x＜y＜z |
如图在四棱锥P一ABCD中，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，BC=2AD，AC与BD交于点O，点M，N分别在线PC、AB上，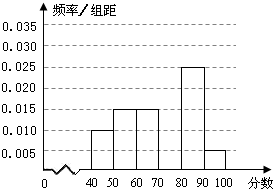
某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题．