Question

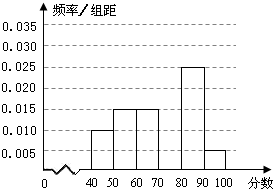某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题．
（Ⅰ）求分数在[70，80）内的频率，并补全这个频率分布直方图；
（Ⅱ）从频率分布直方图中，估计本次考试成绩的中位数；
（Ⅲ）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率．

Answer 1

考点：古典概型及其概率计算公式,频率分布直方图

专题：概率与统计

分析：（I）利用所有小矩形的面积之和为1，求得分数在[70，80）内的频率，再根据小矩形的高=

频率

组距

求得小矩形的高，补全频率分布直方图；
（II）根据中位数的左、右两边的小矩形的面积之和相等，求从左数频率之和等于0.5的横坐标的值；
（III）利用组合数公式计算从从第1组和第6组所有人数中任取2人的取法种数，再计算从第1组与第6组各抽取1人的取法种数，代入古典概型概率公式计算．

解答： 解：（Ⅰ）分数在[70，80）内的频率为1-（0.010+0.015+0.015+0.025+0.005）×10=0.3，
∴小矩形的高为0.030，补全频率分布直方图如图：

（Ⅱ）由频率频率分布直方图知前三组的频率之和为0.1+0.15+0.15=0.4，
∴中位数在第四组，设中位数为70+x，则0.4+0.030×x=0.5⇒x=

10

3

，
∴数据的中位数为70+

10

3

=

220

3

，
（Ⅲ）第1组有60×0.1=6人（设为1，2，3，4，5，6）
第6组有60×0.05=3人（设为A，B，C）
从9人中任取2人有

C

2 9

=36种方法；
其中抽取2人成绩之差的绝对值大于10的抽法是从第1组与第6组各抽取1人，抽法由

C

1 6

×C

1 3

=18种，
∴抽取2人成绩之差的绝对值大于10的概率为

1

2

．

点评：本题考查了利用频率分布直方图求数据的中位数、频数，考查了古典概型的概率计算，在频率分布直方图中频率=小矩形的面积=小矩形的高×组距=

频数

样本容量

．