题目内容
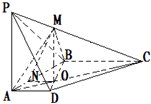
 如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,
如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,| CM |
| MP |
| BN |
| NA |
(Ⅰ)求证:平面MNO∥平面PAD;
(Ⅱ)若平面PA⊥平面ABCD,∠PDA=60°,且PD=DC=BC=2,求几何体M-ABC的体积.
考点:平面与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)在梯形ABCD中依据AD∥BC,推断出0C:OA=BC:AD=2,又由于BN=2NA,继而可知AN∥BC∥AD,在△PAC中,根据比例关系推断出OM∥AP,最后利用面面平行的判定定理证明出平面MNO∥平面PAD;
(Ⅱ)在△PAD中,利用余弦定理求得PA,进而可知PA2+AD2=PD2,推断出PA⊥AD,又根据平面PAD⊥平面ABCD推断出PA⊥平面ABCD,进而证明出MO⊥平面ABC利用MO的值,求得AB,求得底面的面积最后利用体积公式求得几何体M-ABC的体积.
(Ⅱ)在△PAD中,利用余弦定理求得PA,进而可知PA2+AD2=PD2,推断出PA⊥AD,又根据平面PAD⊥平面ABCD推断出PA⊥平面ABCD,进而证明出MO⊥平面ABC利用MO的值,求得AB,求得底面的面积最后利用体积公式求得几何体M-ABC的体积.
解答:
 证明:(Ⅰ)在梯形ABCD中,∵AD∥BC,
证明:(Ⅰ)在梯形ABCD中,∵AD∥BC,
∴0C:OA=BC:AD=2,
又BN=2NA,
∴ON∥BC∥AD,
∵AD?平面PAD,ON?平面PAD,
∴ON∥平面PAD,
在△PAC中,
∵OC:OA=BC:AD=2,CM=2MP,
∴OM∥AP,
AP?平面PAD,OM?平面PAD,
∴OM∥平面PAD,
∵OM?平面OMN,ON?平面OMN,且OM∩ON=0,
∴平面MNO∥平面PAD;
(Ⅱ)在△PAD中,PA2=PD2+AD2-2PD•AD•cos∠PDA=3
∴PA2+AD2=PD2,即PA⊥AD,又平面PAD⊥平面ABCD
∴PA⊥平面ABCD,又由(Ⅰ)知OM∥AP,
∴MO⊥平面ABC
且MO=
AP=
在梯形ABCD中,CD=BC=2AD=2,
∠BAD=90°,
∴AB=
,
∴△ABC的面积S=
AB•BC=
∴几何体M-ABC的体积V=
MO•S=
 证明:(Ⅰ)在梯形ABCD中,∵AD∥BC,
证明:(Ⅰ)在梯形ABCD中,∵AD∥BC,∴0C:OA=BC:AD=2,
又BN=2NA,
∴ON∥BC∥AD,
∵AD?平面PAD,ON?平面PAD,
∴ON∥平面PAD,
在△PAC中,
∵OC:OA=BC:AD=2,CM=2MP,
∴OM∥AP,
AP?平面PAD,OM?平面PAD,
∴OM∥平面PAD,
∵OM?平面OMN,ON?平面OMN,且OM∩ON=0,
∴平面MNO∥平面PAD;
(Ⅱ)在△PAD中,PA2=PD2+AD2-2PD•AD•cos∠PDA=3
∴PA2+AD2=PD2,即PA⊥AD,又平面PAD⊥平面ABCD
∴PA⊥平面ABCD,又由(Ⅰ)知OM∥AP,
∴MO⊥平面ABC
且MO=
| 2 |
| 3 |
2
| ||
| 3 |
在梯形ABCD中,CD=BC=2AD=2,
∠BAD=90°,
∴AB=
| 3 |
∴△ABC的面积S=
| 1 |
| 2 |
| 3 |
∴几何体M-ABC的体积V=
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查了平面与平面平行的判定定理,几何体的体积公式等.考查了学生基础知识的综合运用.

练习册系列答案
相关题目
已知全集U=R,集合A={x||x-2|<1},B={x|y=
},则A∩B=( )
| 4-2x |
| A、(1,2) |
| B、(2,3) |
| C、[2,3) |
| D、(1,2] |