题目内容
已知等差数列{an}的首项a1=-1，公差d=
，则{an}的第一个正数项是（ ）
| 1 |
| 5 |
| A、a4 |
| B、a5 |
| C、a6 |
| D、a7 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：先根据等差数列的通项公式，求得an，令an＞0求得n的范围，即可推断出第一个正数项．
解答：
解：依题意知an=-1+（n-1）•
=
-
，
令an＞0，求得n＞6，
∴数列中第7项为第一个正数项．
故选：D．
| 1 |
| 5 |
| n |
| 5 |
| 6 |
| 5 |
令an＞0，求得n＞6，
∴数列中第7项为第一个正数项．
故选：D．
点评：本题主要考查了等差数列的性质．考查了学生对等差数列通项公式的灵活应用．
练习册系列答案
相关题目
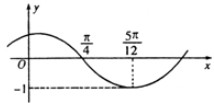f（x）=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
f（x）=x2+lnx，则f′（x）等于（ ）
| A、x+1 | ||
| B、2x+1 | ||
C、x+
| ||
D、2x+
|
若直线l1：y=kx+1与l2：x-y-1=0的交点在第一象限内，则k的取值范围是（ ）
| A、k＞1 |
| B、-1＜k＜1 |
| C、k＜-1或k＞1 |
| D、k＜-1 |
已知a1=1，a2=-
，a3=-
，…，an+1=-
，…．那么a2014=（ ）
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| A、-2 | ||
B、-
| ||
| C、1 | ||
| D、2 |
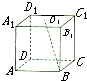如图，正方体A1B1C1D1-ABCD中，O1是上底面A1B1C1D1的中心，若正方体的棱长为2，则O1B与CD所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知两点O（0，0）、A（1，1）及直线l：x+y=a，它们满足：O、A有一点在直线l上或O、A在直线l的两侧．设h（a）=a2+2a+3，则使不等式x2+4x-2≤h（a）恒成立的x的取值范围是（ ）
| A、[0，2] |
| B、[-5，1] |
| C、[3，11] |
| D、[2，3] |