题目内容
已知两点O（0，0）、A（1，1）及直线l：x+y=a，它们满足：O、A有一点在直线l上或O、A在直线l的两侧．设h（a）=a2+2a+3，则使不等式x2+4x-2≤h（a）恒成立的x的取值范围是（ ）
| A、[0，2] |
| B、[-5，1] |
| C、[3，11] |
| D、[2，3] |
考点：二元一次不等式的几何意义
专题：不等式的解法及应用
分析：由题意可得a的范围，进而可得h（a）的最小值，由恒成立可得x的不等式，解不等式可得．
解答：
解：由O、A有一点在直线l上可得a=0或a=2，
由O、A在直线l的两侧可得a（a-2）＜0，
解得0＜a＜2，故0≤a≤2，
又函数h（a）=（a+1）2+2在[0，2]上单调递增，
∴hmax（a）=h（2）=11，hmin（a）=h（0）=3．
由x2+4x-2≤h（a）得x2+4x-2≤3，
解不等式可得得-5≤x≤1．
故选：B
由O、A在直线l的两侧可得a（a-2）＜0，
解得0＜a＜2，故0≤a≤2，
又函数h（a）=（a+1）2+2在[0，2]上单调递增，
∴hmax（a）=h（2）=11，hmin（a）=h（0）=3．
由x2+4x-2≤h（a）得x2+4x-2≤3，
解不等式可得得-5≤x≤1．
故选：B
点评：本题考查二元一次不等式的几何意义，涉及恒成立问题，属基础题．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知等差数列{an}的首项a1=-1，公差d=
，则{an}的第一个正数项是（ ）
| 1 |
| 5 |
| A、a4 |
| B、a5 |
| C、a6 |
| D、a7 |
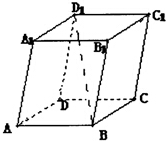
在平行六面体ABCD-A1B1C1D1中，用向量
，
，
来表示向量
为（ ）
| AB |
| AD |
| AA1 |
| BD1 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
某学习小组在一次数学测验中，得100分的有1人，得95分的有1人，得90分的有2人，得85分的有4人，得80分和75分的各有1人，则该小组数学成绩的平均数、众数、中位数分别是（ ）
| A、85，85，85 |
| B、87，85，86 |
| C、87，85，85 |
| D、87，85，90 |
从1、2、3、4、5、6这六个数中，每次取出两个不同数记为a、b，则共可得到3
的不同数值的个数（ ）
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |
如图，在四棱锥P-ABCD中，四边形ABCD是矩形，侧面PAD⊥底面ABCD，若点E，F分别是PC，BD的中点．