题目内容
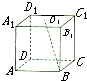如图，正方体A1B1C1D1-ABCD中，O1是上底面A1B1C1D1的中心，若正方体的棱长为2，则O1B与CD所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：异面直线及其所成的角
专题：空间角
分析：过O1作O1P∥CD，交棱B1C1于点P，连结BP，则∠BO1P就是O1B与CD所成角．由此能求出结果．
解答：
解：如图，过O1
作O1P∥CD，交棱B1C1于点P，连结BP，
则∠BO1P就是O1B与CD所成角，
∵正方体的棱长为2，O1是上底面A1B1C1D1的中心，
∴P是B1C1中点，O1P=1，BP=
=
，O1P⊥BP1，
∴BO1=
=
，
∴cos∠BO1P=
=
=
．
故选：D．
作O1P∥CD，交棱B1C1于点P，连结BP，则∠BO1P就是O1B与CD所成角，
∵正方体的棱长为2，O1是上底面A1B1C1D1的中心，
∴P是B1C1中点，O1P=1，BP=
| 22+12 |
| 5 |
∴BO1=
| 5+1 |
| 6 |
∴cos∠BO1P=
| O1P |
| O1B |
| 1 | ||
|
| ||
| 6 |
故选：D．
点评：本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
已知等差数列{an}的首项a1=-1，公差d=
，则{an}的第一个正数项是（ ）
| 1 |
| 5 |
| A、a4 |
| B、a5 |
| C、a6 |
| D、a7 |
下列说法正确的是（ ）
| A、命题“若x2-5x+6=0，则x=2”的逆命题是“若x≠2，则x2-5x+6≠0” |
| B、命题“若x=2，则x2-5x+6=0”的否命题是“若x=2，则x2-5x+6≠0” |
| C、已知a，b∈R，则“a＞b”是“|a|＞|b|”的充要条件 |
| D、已知a，b∈R，则“ab≠0”是“a≠0”的充分条件 |
已知Rt△ABC的两条直角边的边长分别为3和4，若以其中一条直角边为轴旋转一周，则所形成的几何体的体积为（ ）
| A、16π |
| B、12π或16π |
| C、36π |
| D、36π或48π |
在平行六面体ABCD-A1B1C1D1中，用向量
，
，
来表示向量
为（ ）
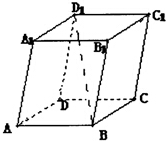
| AB |
| AD |
| AA1 |
| BD1 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
某学习小组在一次数学测验中，得100分的有1人，得95分的有1人，得90分的有2人，得85分的有4人，得80分和75分的各有1人，则该小组数学成绩的平均数、众数、中位数分别是（ ）
| A、85，85，85 |
| B、87，85，86 |
| C、87，85，85 |
| D、87，85，90 |