题目内容
 f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<
f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由参数的意义易得函数的解析式,由函数图象变换的法则可得.
解答:
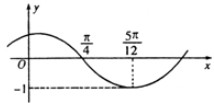
解:由图象可得A=1,
=
-
=
,
解得ω=3,∴f(x)=sin(3x+φ)
∵图象过(
,0),∴
+φ=π∴φ=
,
∴f(x)=sin(3x+
)=sin[3(x+
)]
∴为得到g(x)=sin3x的图象,需将f(x)的图象右移
个单位即可.
故选:C
| 2π |
| 4ω |
| 5π |
| 12 |
| π |
| 4 |
| π |
| 6 |
解得ω=3,∴f(x)=sin(3x+φ)
∵图象过(
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴f(x)=sin(3x+
| π |
| 4 |
| π |
| 12 |
∴为得到g(x)=sin3x的图象,需将f(x)的图象右移
| π |
| 12 |
故选:C
点评:本题考查三角函数解析式得求解,以及函数图象的变换,属基础题.

练习册系列答案
相关题目
在高台跳水运动中,已知运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10,则运动员在t=1s时的瞬间速度为( )
| A、3.3m/s |
| B、-3.3m/s |
| C、11.6m/s |
| D、-11.6m/s |
函数y=ln(1-x)+
的定义域为( )
| x |
| A、{x|x≥0} |
| B、{x|x≤1} |
| C、{x|0<x≤1} |
| D、{x|0≤x<1} |
若4-3a-a2i=a2+4ai(i为虚数单位),则实数a的值为( )
| A、4 | B、0 | C、-4 | D、0或-4 |
已知等差数列{an}的首项a1=-1,公差d=
,则{an}的第一个正数项是( )
| 1 |
| 5 |
| A、a4 |
| B、a5 |
| C、a6 |
| D、a7 |
下列说法正确的是( )
| A、命题“若x2-5x+6=0,则x=2”的逆命题是“若x≠2,则x2-5x+6≠0” |
| B、命题“若x=2,则x2-5x+6=0”的否命题是“若x=2,则x2-5x+6≠0” |
| C、已知a,b∈R,则“a>b”是“|a|>|b|”的充要条件 |
| D、已知a,b∈R,则“ab≠0”是“a≠0”的充分条件 |
某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各有1人,则该小组数学成绩的平均数、众数、中位数分别是( )
| A、85,85,85 |
| B、87,85,86 |
| C、87,85,85 |
| D、87,85,90 |