题目内容
11.若函数$f(x)=\sqrt{2}cos({ωx+\frac{π}{4}})$在x=0处的切线方程为y=-3x+1,则ω=3.分析 求出f(x)的导数,可得x=0处切线的斜率,由已知切线的方程即可得到所求值.
解答 解:函数$f(x)=\sqrt{2}cos({ωx+\frac{π}{4}})$的导数为f′(x)=-$\sqrt{2}$ωsin(ωx+$\frac{π}{4}$),
可得在x=0处的切线斜率为-$\sqrt{2}$ωsin$\frac{π}{4}$=-$\sqrt{2}$?•$\frac{\sqrt{2}}{2}$=-ω,
由在x=0处的切线方程为y=-3x+1,可得-ω=-3,
可得ω=3,
故答案为:3.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,正确求导和运用直线方程是解题的关键,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
1.王明参加某卫视的闯关活动,该活动共3关.设他通过第一关的概率为0.8,通过第二、第三关的概率分别为p,q,其中p>q,并且是否通过不同关卡相互独立.记ξ为他通过的关卡数,其分布列为:
(Ⅰ)求王明至少通过1个关卡的概率;
(Ⅱ)求p,q的值.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.048 | a | b | 0.192 |
(Ⅱ)求p,q的值.
16.圆的任何一对平行切线间的距离总是相等的,即圆在任意方向都有相同的宽度,具有这种性质的曲线可称为“等宽曲线”.事实上存在着大量的非圆等宽曲线,以工艺学家鲁列斯( Reuleaux)命名的鲁列斯曲边三角形,就是著名的非圆等宽曲线.它的画法(如图1):画一个等边三角形ABC,分别以A,B,C为圆心,边长为半径,作圆弧$\widehat{BC},\widehat{CA},\widehat{AB}$,这三段圆弧围成的图形就是鲁列斯曲边三角形.它的宽度等于原来等边三角形的边长.等宽曲线都可以放在边长等于曲线宽度的正方形内(如图2).

在图2中的正方形内随机取一点,则这一点落在鲁列斯曲边三角形内的概率为( )

在图2中的正方形内随机取一点,则这一点落在鲁列斯曲边三角形内的概率为( )
| A. | $\frac{π}{8}$ | B. | $\frac{{2π-3\sqrt{3}}}{4}$ | C. | $\frac{{π-\sqrt{2}}}{2}$ | D. | $\frac{{π-\sqrt{3}}}{2}$ |
3.已知点M(-1,0)和N(-1,0),若某直线上存在点p,使得|PM|+|PN|=4,则称该直线为“椭型直线”.现有下列直线:
①x-2y+6=0
②x-y=0
③2x-y+1=0
④x+y-3=0
其中是“椭型直线”的是( )
①x-2y+6=0
②x-y=0
③2x-y+1=0
④x+y-3=0
其中是“椭型直线”的是( )
| A. | ①③ | B. | ①② | C. | ②③ | D. | ③④ |
1.已知向量$\overrightarrow{m}$=(-1,2),$\overrightarrow{n}$=(1,λ),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则$\overrightarrow{m}$+2$\overrightarrow{n}$与$\overrightarrow{m}$的夹角为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
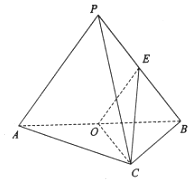 已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.
已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.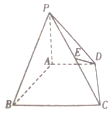 如图,在底面为直角梯形的四棱锥P-ABCD中,E为PC的中点,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=2,AD=2,AB=2$\sqrt{3}$,BC=4.
如图,在底面为直角梯形的四棱锥P-ABCD中,E为PC的中点,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=2,AD=2,AB=2$\sqrt{3}$,BC=4.