题目内容
6.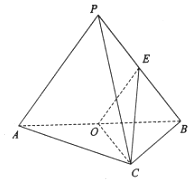 已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.
已知三棱锥P-ABC中,AC⊥BC,AC=BC=2,PA=PB=BC=3,O是AB中点,E是PB中点.(1)证明:平面PAB⊥平面ABC;
(2)求点B到平面OEC的距离.
分析 (1)连结PO,推导出PO⊥AB,AC⊥BC,PO⊥OC.从而PO⊥平面ABC,由此能证明平面PAB⊥平面ABC.
(2)推导出$OE=\frac{3}{2}$,OC⊥AB,从而OC⊥平面PAB,进而OC⊥OE.设点B到平面OEC的距离为d,由VB-OEC=VE-OBC,能求出点B到平面OEC的距离.
解答 证明:(1)连结PO,在△PAB中,PA=PB,O是AB中点,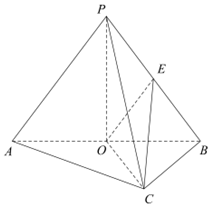
∴PO⊥AB,
又∵AC=BC=2,AC⊥BC,∴$AB=2\sqrt{2},OB=OC=\sqrt{2}$.
∵PA=PB=BC=3,∴$PO=\sqrt{7}$,PC2=PO2+OC2,
∴PO⊥OC.
又AB∩OC=O,AB?平面ABC,OC?平面ABC,
∴PO⊥平面ABC,
∵PO?平面PAB,∴平面PAB⊥平面ABC.
解:(2)∵OE是△PAB的中位线,∴$OE=\frac{3}{2}$.
∵O是AB中点,AC=BC,∴OC⊥AB.
又平面PAB⊥平面ABC,两平面的交线为AB,∴OC⊥平面PAB,
∵OE?平面PAB,∴OC⊥OE.
设点B到平面OEC的距离为d,则VB-OEC=VE-OBC,
∴$\frac{1}{3}×{S_{△OEC}}•d=\frac{1}{3}×{S_{△OBC}}×\frac{1}{2}OP$,
∴点B到平面OEC的距离:
$d=\frac{{{S_{△OBC}}•\frac{1}{2}OP}}{{{S_{△OEC}}}}=\frac{{\frac{1}{2}OB•OC•\frac{1}{2}OP}}{{\frac{1}{2}OE•OC}}=\frac{{\sqrt{14}}}{3}$.
点评 本题考查面面垂直的证明,考查点到平面的距离的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案| A. | (0,e] | B. | {0,e} | C. | {1,2} | D. | (1,2) |
| A. | $\frac{1}{2}i$ | B. | $-\frac{1}{2}i$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 第三产业比重y(%) | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
(2)建立第三产业在GDP中的比重y关于年份代码x的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在GDP中的比重.
附注:回归直线方程$\widehaty=\widehata+\widehatbx$中的斜率和截距的最小二乘估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.