题目内容
20.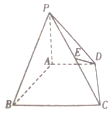 如图,在底面为直角梯形的四棱锥P-ABCD中,E为PC的中点,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=2,AD=2,AB=2$\sqrt{3}$,BC=4.
如图,在底面为直角梯形的四棱锥P-ABCD中,E为PC的中点,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=2,AD=2,AB=2$\sqrt{3}$,BC=4.(1)求证:DE∥平面PAB;
(2)求直线AE与平面PCD所成角的正弦值.
分析 (1)取BC中点F,连接DF,EF,证明:平面DEF∥平面PAB,即可证明DE∥平面PAB;
(2)建立坐标系,利用向量的方法求直线AE与平面PCD所成角的正弦值.
解答 (1)证明:取BC中点F,连接DF,EF.
因为四边形ABCD是直角梯形,∴DF∥AB
又∵FE∥PB,∴平面DEF∥平面PAB,
∵DE?平面DEF,
∴DE∥平面PAB;
(2)解:建立如图空间直角坐标系,
则$A(0,0,0),P(0,0,2),D(0,2,0),C(2\sqrt{3},4,0),E(\sqrt{3},2,1)$
∴$\overrightarrow{AE}$=($\sqrt{3}$,2,1),$\overrightarrow{PD}$=(0,2,-2),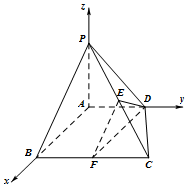
$\overrightarrow{DC}$=(2$\sqrt{3}$,2,0),
设$\overrightarrow n=(x,y,z)$是平面PCD的一个法向量.
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{PD}=0\\ \overrightarrow n•\overrightarrow{DC}=0\end{array}\right.⇒\overrightarrow n=(1,-\sqrt{3},-\sqrt{3})$,
∴sinθ=|$\frac{\sqrt{3}-2\sqrt{3}-\sqrt{3}}{\sqrt{8}•\sqrt{7}}$|=$\frac{\sqrt{42}}{14}$.
点评 本题考查了直线与平面平行的判定,考查了求线面角的方法,考查向量方法的运用,属中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
5.等比数列{an}中,a1+a3=10,a2+a4=30,则数列{an}前5项和S5=( )
| A. | 81 | B. | 90 | C. | 100 | D. | 121 |
9.设集合A={x|x2-3x-4≤0},B={x||x|≤3},则集合A∩B=( )
| A. | [-3,-1] | B. | [-3,4] | C. | [-1,3] | D. | [3,4] |