题目内容
3.已知点M(-1,0)和N(-1,0),若某直线上存在点p,使得|PM|+|PN|=4,则称该直线为“椭型直线”.现有下列直线:①x-2y+6=0
②x-y=0
③2x-y+1=0
④x+y-3=0
其中是“椭型直线”的是( )
| A. | ①③ | B. | ①② | C. | ②③ | D. | ③④ |
分析 由题意可知,点P的轨迹是以M,N为焦点的椭圆,把直线方程分别代入椭圆方程看是否有解即可判断出结论.
解答 解:由椭圆的定义可知,点P的轨迹是以M,N为焦点的椭圆,其方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,
对于①,把x-2y+6=0代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,并整理得16y2-68y+96=0,由△=682-4×16×(96)=-1520<0,
则x-2y+6=0不是椭型直线”;
对于②,把y=x代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,解得:x2=$\frac{12}{7}$成立,
∴x-y=0是“椭型直线”;
对于③,把2x-y+1=0代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,19x2+16x-8=0,由△=(16)2-4×19×(-8)>0,
则2x-y+1=0是“椭型直线”
对于④把x+y-3=0代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,7x2-24x+24=0,△=(-24)2-4×7×24<0,
则y=-x+3不是“椭型直线”;
故②③是“椭型直线”,
故选C.
点评 本题是新定义题,考查了椭圆的定义及标准方程,考查了数学转化思想方法及方程思想方法,解答此题的关键是把问题转化为判断直线方程与椭圆方程联立的方程组是否有解,属中档题.

练习册系列答案
相关题目
18. 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
(1)在所给坐标系中作出数据对应的散点图;
(2)建立第三产业在GDP中的比重y关于年份代码x的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在GDP中的比重.
附注:回归直线方程$\widehaty=\widehata+\widehatbx$中的斜率和截距的最小二乘估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
 根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:
根据“2015年国民经济和社会发展统计公报”中公布的数据,从2011 年到2015 年,我国的第三产业在GDP中的比重如下:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代码x | 1 | 2 | 3 | 4 | 5 |
| 第三产业比重y(%) | 44.3 | 45.5 | 46.9 | 48.1 | 50.5 |
(2)建立第三产业在GDP中的比重y关于年份代码x的回归方程;
(3)按照当前的变化趋势,预测2017 年我国第三产业在GDP中的比重.
附注:回归直线方程$\widehaty=\widehata+\widehatbx$中的斜率和截距的最小二乘估计公式分别为:$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
13.若复数z满足$(1+i)z=|{\sqrt{3}+i}|$,则在复平面内,$\overline z$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
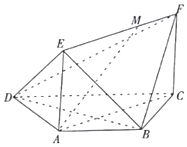 如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.
如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.