题目内容
试证明函数f(x)=x2在(0,+∞)上是单调增函数.
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据函数单调性的定义即可证明函数的单调性.
解答:
证明:设任意的x1,x2∈(0,+∞),且x1<x2,
所以有f(x1)-f(x2)=x12-x22=(x1+x2)(x1-x2),
因为0<x1<x2,
所以x1-x2<0,x1+x2>0,
所以f(x1)-f(x2)<0,
即f(x1)<f(x2),
故函数y=x2在x∈(0,+∞)是单调递增函数.
所以有f(x1)-f(x2)=x12-x22=(x1+x2)(x1-x2),
因为0<x1<x2,
所以x1-x2<0,x1+x2>0,
所以f(x1)-f(x2)<0,
即f(x1)<f(x2),
故函数y=x2在x∈(0,+∞)是单调递增函数.
点评:本题考查函数单调性的判断与证明,要求熟练掌握利用定义证明函数的单调性.

练习册系列答案
相关题目
下列叙述错误的是( )
| A、频率是随机的,在试验前不能确定,随着试验次数的增加,频率一般会越来越接近概率 | ||
| B、互斥事件不一定是对立事件,但是对立事件一定是互斥事件 | ||
| C、若随机事件A发生的概率为p(A),则0≤p(A)≤1 | ||
D、某种彩票(有足够多)中奖概率为
|
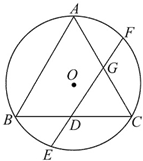 如图,△ABC是⊙O的内接正三角形,弦EF经过BC的中点D,且EF∥AB,若AB=2,则DE的长是
如图,△ABC是⊙O的内接正三角形,弦EF经过BC的中点D,且EF∥AB,若AB=2,则DE的长是