题目内容
已知函数f(x)=
,若方程f(x)-kx=0恰有两个不同的实根时,则实数k的取值范围是(其中e为自然对数的底数)( )
|
| A、(1,e) |
| B、[1,3] |
| C、(3,+∞) |
| D、(e,3] |
考点:分段函数的应用
专题:数形结合,函数的性质及应用
分析:画出函数f(x)的图象和y=kx的图象,观察直线绕原点旋转时,与曲线y=ex相切,和y=3x-1平行的情况,设出切点,列出方程,求出切线的斜率,然后观察即可得到k的取值范围.
解答:
解:画出函数f(x)的图象和y=kx的图象,
 观察直线绕原点旋转时,与曲线y=ex相切,和y=3x-1平行的情况,
观察直线绕原点旋转时,与曲线y=ex相切,和y=3x-1平行的情况,
令切点为(m,n),则n=em,em=k,n=km
解得m=1,n=e,k=e,
通过图象观察当k>3时,有三个交点,
当e<k≤3时,有两个交点.
故方程f(x)-kx=0恰有两个不同的实根时,
则实数k的取值范围是(e,3].
故选D.
 观察直线绕原点旋转时,与曲线y=ex相切,和y=3x-1平行的情况,
观察直线绕原点旋转时,与曲线y=ex相切,和y=3x-1平行的情况,令切点为(m,n),则n=em,em=k,n=km
解得m=1,n=e,k=e,
通过图象观察当k>3时,有三个交点,
当e<k≤3时,有两个交点.
故方程f(x)-kx=0恰有两个不同的实根时,
则实数k的取值范围是(e,3].
故选D.
点评:本题考查分段函数的图象及运用,考查方程的根的个数转化为函数的图象交点个数,考查数形结合的能力,属于中档题.

练习册系列答案
相关题目
下列叙述错误的是( )
| A、频率是随机的,在试验前不能确定,随着试验次数的增加,频率一般会越来越接近概率 | ||
| B、互斥事件不一定是对立事件,但是对立事件一定是互斥事件 | ||
| C、若随机事件A发生的概率为p(A),则0≤p(A)≤1 | ||
D、某种彩票(有足够多)中奖概率为
|
函数f(x)=x3+x-1在(0,4)上零点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知角2α的终边在x轴的上方,那么α是( )
| A、第一象限角 |
| B、第一、二象限角 |
| C、第一、三象限角 |
| D、第一、四象限角 |
已知A(-2,-3),B(2,1),C(1,4),D(-7,-4),则有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f′(x)≥0,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 98 |
| 19 |
| 101 |
| 17 |
| 106 |
| 15 |
| A、c<b<a |
| B、c<a<b |
| C、a<c<b |
| D、a<b<c |
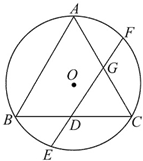 如图,△ABC是⊙O的内接正三角形,弦EF经过BC的中点D,且EF∥AB,若AB=2,则DE的长是
如图,△ABC是⊙O的内接正三角形,弦EF经过BC的中点D,且EF∥AB,若AB=2,则DE的长是