题目内容
2．若实数x，y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{x+2y-4≥0}\\{2x+y-5≤0}\end{array}\right.$且3（x-a）+2（y+1）的最大值为5，则a等于（ ）| A． | -2 | B． | -1 | C． | 2 | D． | 1 |
分析 画出约束条件的可行域，利用目标函数的几何意义，在可行域中找出最优点，然后求解即可．
解答 
解：实数x，y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{x+2y-4≥0}\\{2x+y-5≤0}\end{array}\right.$，不是的可行域如图：
3（x-a）+2（y+1）=3x+2y+2-3a的最大值为：5，由可行域可知z=3x+2y+2-3a，经过A时，z取得最大值，
由$\left\{\begin{array}{l}{x-y+2=0}\\{2x+y-5=0}\end{array}\right.$，可得A（1，3）可得3+6+2-3a=5，
解得a=2．
故选：C．
点评 本题考查线性规划的简单应用，考查目标函数的最值的求法，考查数形结合以及转化思想的应用．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
12．已知函数y=f（x）（x∈R）且在[0，+∞）上是增函数，g（x）=f（|x|），若g（2x-1）＜g（2），则x的取值范围是（ ）
| A． | （-$\frac{1}{2}$，$\frac{3}{2}$） | B． | （-∞，$\frac{3}{2}$） | C． | （$\frac{3}{2}$，+∞） | D． | （-∞，$-\frac{1}{2}$）∪（$\frac{3}{2}$，+∞） |
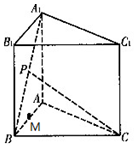已知正三棱柱ABC-A1B1C的各条棱长都为a，P为A1B的中点，M为AB的中点，
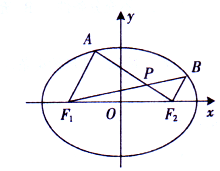设F1，F2是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），的左右焦点，离心率为$\frac{\sqrt{2}}{2}$，M为椭圆上的动点，|MF1|的最大值为1$+\sqrt{2}$．