题目内容
14.已知点P($\sqrt{2}$,1)和椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1.(1)设椭圆的两个焦点分别为F1,F2,试求△PF1F2的周长及椭圆的离心率;
(2)若直线l:$\sqrt{2}$x-2y+m=0(m≠0)与椭圆C交于两个不同的点A,B,设直线PA与PB的斜率分别为k1,k2,求证:k1+k2=0.
分析 (1)求得椭圆的a,b,c,可得P在椭圆上,运用椭圆的定义,即可得到△PF1F2的周长和椭圆的离心率;
(2)联立直线和椭圆方程,可得x的二次方程,运用判别式大于0,以及韦达定理,结合直线的斜率公式,化简整理,即可得证.
解答 解:(1)椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的a=2,b=$\sqrt{2}$,c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2}$,
点P($\sqrt{2}$,1)在椭圆C上,由椭圆定义可得|PF1|+|PF2|=2a=4,
△PF1F2的周长为2a+2c=4+2$\sqrt{2}$;
椭圆的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$;
(2)证明:联立直线$\sqrt{2}$x-2y+m=0和椭圆x2+2y2=4,
可得4x2+2$\sqrt{2}$mx+m2-8=0,
由直线与椭圆有两个交点,且直线不过点P,
可得△=8m2-4×4(m2-8)>0,且m≠0,
解得-4<m<0或0<m<4.
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{\sqrt{2}}{2}$m,x1x2=$\frac{{m}^{2}-8}{4}$,
y1=$\frac{\sqrt{2}{x}_{1}+m}{2}$,y2=$\frac{\sqrt{2}{x}_{2}+m}{2}$,
则k1+k2=$\frac{{y}_{1}-1}{{x}_{1}-\sqrt{2}}$+$\frac{{y}_{2}-1}{{x}_{2}-\sqrt{2}}$=$\frac{\sqrt{2}{x}_{1}+m-2}{2({x}_{1}-\sqrt{2})}$+$\frac{\sqrt{2}{x}_{2}+m-2}{2({x}_{2}-\sqrt{2})}$
=$\sqrt{2}$+$\frac{m}{2({x}_{1}-\sqrt{2})}$+$\frac{m}{2({x}_{2}-\sqrt{2})}$=$\sqrt{2}$+$\frac{m({x}_{1}+{x}_{2})-2\sqrt{2}m}{2({x}_{1}-\sqrt{2})({x}_{2}-\sqrt{2})}$
=$\sqrt{2}$+$\frac{-\frac{\sqrt{2}}{2}{m}^{2}-2\sqrt{2}m}{2(\frac{{m}^{2}-8}{4}+2+m)}$=$\sqrt{2}$-$\sqrt{2}$•$\frac{\frac{1}{2}{m}^{2}+2m}{\frac{1}{2}{m}^{2}+2m}$=0.
点评 本题考查椭圆的定义、方程和性质,考查直线和椭圆方程联立,运用韦达定理,同时考查直线的斜率公式,考查化简整理的运算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | 12 | B. | 4 | C. | 6 | D. | 2 |
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
| A. | ($\frac{1}{4}$,1) | B. | (2,+∞) | C. | $({-∞,-2})∪({\frac{1}{4},+∞})$ | D. | $({-∞,\frac{1}{4}})$ |
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)是减函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |
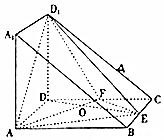 将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.
将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.