题目内容
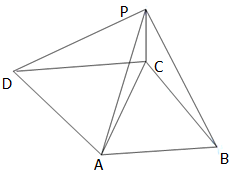
底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
a,求证:PA⊥平面ABCD.
| 2 |

考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:要证PA⊥平面ABCD,只需证明直线PA垂直平面ABCD内的两条相交直线AB、AD即可.
解答:
证明: ∵底面ABCD是菱形,且∠ABC=60°,
∵底面ABCD是菱形,且∠ABC=60°,
∴AB=AD=AC=a,
在△PAB中,PA2+AB2=2a2=PB2,
∴∠PAB=90°,即PA⊥AB,
同理,PA⊥AD,
∵AB∩AD=A,
∴PA⊥平面ABCD.
 ∵底面ABCD是菱形,且∠ABC=60°,
∵底面ABCD是菱形,且∠ABC=60°,∴AB=AD=AC=a,
在△PAB中,PA2+AB2=2a2=PB2,
∴∠PAB=90°,即PA⊥AB,
同理,PA⊥AD,
∵AB∩AD=A,
∴PA⊥平面ABCD.
点评:本题考查直线与平面垂直的判定,考查空间想象能力,逻辑思维能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若A={x|x(x-3)≥0},函数y=ln(x-1)的定义域为集合B,则A∩B=( )
| A、(1,3] |
| B、(1,+∞) |
| C、(3,+∞) |
| D、[3,+∞) |
曲线y=4lnx-x2在点A(1,-1)处的切线的斜率是( )
| A、4 | B、3 | C、2 | D、1 |
 如图给出了函数:y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数依次对应的图象是( )
如图给出了函数:y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数依次对应的图象是( )| A、①②③④ | B、①③②④ |
| C、②③①④ | D、①④③② |