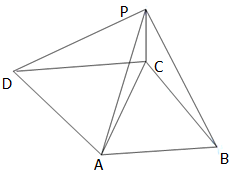
题目内容
若PA⊥平面ABCD，且ABCD是矩形，若PA=3，AB=2，BC=2
，则二面角P-BD-A的正切值为 ．
| 3 |
考点：二面角的平面角及求法
专题：空间角
分析：利用PA⊥面ABCD，通过由三垂线定理法作出二面角，过A做AH⊥BD与H，连接PH即可，再在直角△PHB中求解．
解答：
解：过A作AH⊥BD与H，连接PH，因为PA⊥面ABCD，所以∠PHA即为二面角P-BD-A的平面角．
在直角△PHB中，因为PA=3，AB=2，BC=2
，BD=
=4，
AH=
=
=
，
所以tan∠PHA=
=
=
．
故答案为：
．
解：过A作AH⊥BD与H，连接PH，因为PA⊥面ABCD，所以∠PHA即为二面角P-BD-A的平面角．在直角△PHB中，因为PA=3，AB=2，BC=2
| 3 |
22+(2
|
AH=
| AB×AD |
| BD |
2×2
| ||
| 4 |
| 3 |
所以tan∠PHA=
| PA |
| AH |
| 3 | ||
|
| 3 |
故答案为：
| 3 |
点评：本题考查三垂线定理法求二面角，考查空间想象能力，属于基本知识的考查．
练习册系列答案
53随堂测系列答案
相关题目
若从5名男歌手和4名女歌手中各选一人参加“星光大道”节目，则不同的选法种数是（ ）
| A、5种 | B、4种 | C、9种 | D、20种 |
已知椭圆
+
=1的两个焦点为F1，F2，弦AB过点F1，则△ABF2的周长为（ ）
| x2 |
| 41 |
| y2 |
| 25 |
| A、10 | ||
| B、20 | ||
C、2
| ||
D、4
|
