题目内容
设f(x)=x+1,那么f(x+1)关于直线x=2对称的曲线的解析式是( )
| A、y=x-6 |
| B、y=6+x |
| C、y=6-x |
| D、y=-x-2 |
考点:函数解析式的求解及常用方法
专题:数形结合法,函数的性质及应用
分析:根据f(x)的解析式得出f(x+1)的解析式,画出图象,结合图形,求出该曲线关于直线x=2对称的曲线方程即可.
解答:
解:∵f(x)=x+1,
∴f(x+1)=(x+1)+1=x+2;
设该函数的图象关于直线x=2对称的曲线为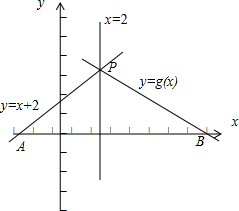
y=g(x)=kx+b,如图所示;
又y=x+2与x轴的交点为A(-2,0),与x=2的交点为P(2,4),
且A点关于x=2的对称点为B(6,0);
∴
,
解得k=-1、b=6;
∴曲线y=g(x)的解析式是g(x)=-x+6.
故选:C.
∴f(x+1)=(x+1)+1=x+2;
设该函数的图象关于直线x=2对称的曲线为
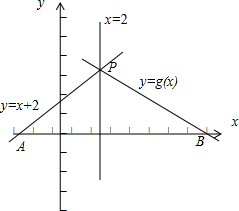
y=g(x)=kx+b,如图所示;
又y=x+2与x轴的交点为A(-2,0),与x=2的交点为P(2,4),
且A点关于x=2的对称点为B(6,0);
∴
|
解得k=-1、b=6;
∴曲线y=g(x)的解析式是g(x)=-x+6.
故选:C.
点评:本题考查了函数图象的平移与对称的应用问题,也考查了数形结合的应用问题,是基础题目.

练习册系列答案
相关题目
log23,log35,3-2的大小关系正确的是( )
| A、log23>log35>3-2 |
| B、log23>3-2>log35 |
| C、log35>log23>3-2 |
| D、3-2>log35>log23 |
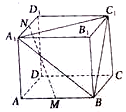 如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?
如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?