题目内容
已知log2(x+y)=log2x+log2y,则
+
= ,x+2y的最小值为 .
| 1 |
| x |
| 1 |
| y |
考点:基本不等式
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由对数的性质:同底的对数的和即为积的对数,化简整理可得x,y的倒数和,再由1的代换,结合基本不等式,即可得到最小值.
解答:
解:log2(x+y)=log2x+log2y即为
log2(x+y)=log2(xy),
即有x+y=xy,
则
+
=1;
即有x+2y=(x+2y)×1=(x+2y)•(
+
)=3+
+
(x,y>0)
≥3+2
=3+2
.
当且仅当x=
y取得最小值3+2
.
故答案为:1,3+2
.
log2(x+y)=log2(xy),
即有x+y=xy,
则
| 1 |
| x |
| 1 |
| y |
即有x+2y=(x+2y)×1=(x+2y)•(
| 1 |
| x |
| 1 |
| y |
| x |
| y |
| 2y |
| x |
≥3+2
|
| 2 |
当且仅当x=
| 2 |
| 2 |
故答案为:1,3+2
| 2 |
点评:本题考查对数的运算性质,考查基本不等式的运用:求最值,考查运算能力,属于基础题和易错题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
给出下列命题:
(1)设随机变量X~N(1,52),且P(X≤0)=P(X>a-2),则实数a的值为4.
(2)已知事件A、B是相互独立事件,若P(A)=0.15,P(B)=0.60,则P(
B)=0.51(
表示事件A的对立事件).
(3)(
+
)18的二项展开式中,共有4个有理项.
(4)由曲线y=3-x2和直线y=2x所围成的面积为
.
则其中真命题的序号是( )
(1)设随机变量X~N(1,52),且P(X≤0)=P(X>a-2),则实数a的值为4.
(2)已知事件A、B是相互独立事件,若P(A)=0.15,P(B)=0.60,则P(
. |
| A |
. |
| A |
(3)(
| 3 | x |
| 1 | ||
|
(4)由曲线y=3-x2和直线y=2x所围成的面积为
| 32 |
| 3 |
则其中真命题的序号是( )
| A、(1)、(2) |
| B、(1)、(3) |
| C、(2)、(3) |
| D、(1)、(2)、(3)、(4) |
△ABC内角A,B,C的对边分别为a,b,c.已知a=3,A=60°,b=
,则B=( )
| 6 |
| A、45° | B、30° |
| C、60° | D、135° |
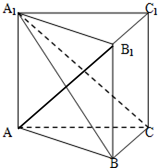 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.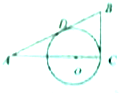 如图,AB和BC分别于圆O相切于点D,C,AC经过圆心O,且BC=2OC=4,则sinA=
如图,AB和BC分别于圆O相切于点D,C,AC经过圆心O,且BC=2OC=4,则sinA=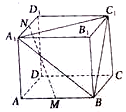 如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?
如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?