题目内容
时下休闲广场活动流行一种“套圈”的游戏,花1元钱可以买到2个竹制的圆形套圈,玩家站在指定的位置向放置在地面上奖品抛掷,一次投掷一个,只要奖品被套圈套住,则该奖品即归玩家所有.已知玩家对一款玩具熊志在必得,玩具被套走以后商家马上更换同样的玩具供玩家游戏,假设玩家发挥稳定且每次投掷套中奖品的概率为0.2.
(1)求投掷第3次才获取玩具熊的概率;
(2)现在用变量X表示获取玩具熊的个数,已知玩家共消费2元,求X的分布列与数学期望与方差.
(1)求投掷第3次才获取玩具熊的概率;
(2)现在用变量X表示获取玩具熊的个数,已知玩家共消费2元,求X的分布列与数学期望与方差.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)投掷第3次才获取玩具熊,是指第一次和第二次均没有投掷套中奖品,且第三次投掷套中奖品,由此能求出投掷第3次才获取玩具熊的概率.
(2)由已知得X=0,1,2,3,4,X~B(4,0.2),由此能求出X的分布列与数学期望与方差.
(2)由已知得X=0,1,2,3,4,X~B(4,0.2),由此能求出X的分布列与数学期望与方差.
解答:
解:(1)投掷第3次才获取玩具熊,是指第一次和第二次均没有投掷套中奖品,
且第三次投掷套中奖品,
∴投掷第3次才获取玩具熊的概率:
P=(1-0.2)(1-0.2)•0.2=0.128.
(2)由已知得X=0,1,2,3,4,
X~B(4,0.2),
P(X=0)=
(0.8)4=0.4096,
P(X=1)=
0.2•(0.8)3=0.4096,
P(X=2)=
(0.2)2•(0.8)2=0.1536,
P(X=3)=
(0.2)3•0.8=0.0256,
P(X=4)=
(0.2)4=0.0004,
∴X的分布列为:
EX=4×0.2=0.8,
DX=4×0.2×(1-0.2)=0.64.
且第三次投掷套中奖品,
∴投掷第3次才获取玩具熊的概率:
P=(1-0.2)(1-0.2)•0.2=0.128.
(2)由已知得X=0,1,2,3,4,
X~B(4,0.2),
P(X=0)=
| C | 0 4 |
P(X=1)=
| C | 1 4 |
P(X=2)=
| C | 2 4 |
P(X=3)=
| C | 3 4 |
P(X=4)=
| C | 4 4 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.4096 | 0.4096 | 0.1536 | 0.0256 | 0.0004 |
DX=4×0.2×(1-0.2)=0.64.
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望、方差的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)单调递增,则f(x)>0的解集为( )
| A、{x|x<0或x>4} |
| B、{x|-2<x<2} |
| C、{x|x>2或x<-2} |
| D、{x|0<x<4} |
幂函数f(x)=xα的图象经过点(2,4),则f(9)=( )
| A、1 | B、3 | C、9 | D、81 |
设复数z=1+2i(i为虚数单位),则z2-
等于( )
| 5 |
| z |
| A、4+6i | ||||
| B、-4+6i | ||||
C、
| ||||
| D、-4+2i |
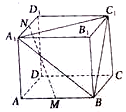 如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?
如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?