题目内容
已知函数f（x）=2|x|的定义域为[a，b]（a＜b），值域为[1，4]，则在平面直角坐标系内，点（a，b）的运动轨迹与两坐标轴围成的图形的面积为（ ）
| A、8 | B、6 | C、4 | D、2 |
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：对于函数f（x）=x2+1而言，当x=±2时，y=5，从而结合题意得出a，b的取值范围．点（a，b）的运动轨迹是两条线段，与两坐标轴围成的图形是一个边长为2的正方形，从而得出结果．
解答：
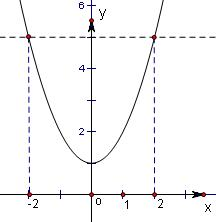解：对于函数f（x）=2|x|，当x=±2时，y=4．
故根据题意得a，b的取值范围为：-2≤a≤0且b=2或a=-2且0≤b≤2．
∴点（a，b）的运动轨迹与两坐标轴围成的图形是一个边长为2的正方形面积为4．
故选：C．
解：对于函数f（x）=2|x|，当x=±2时，y=4．故根据题意得a，b的取值范围为：-2≤a≤0且b=2或a=-2且0≤b≤2．
∴点（a，b）的运动轨迹与两坐标轴围成的图形是一个边长为2的正方形面积为4．
故选：C．
点评：本题考查点（a，b）的运动轨迹与两坐标轴围成的图形的面积，考查运算求解能力，考查数形结合思想．属于基础题．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
执行如图所示的程序框图，则输出的s的值等于（ ）
| A、13 | B、15 | C、36 | D、49 |
函数周期为π，其图象的一条对称轴是x=
，则此函数的解析式可以为（ ）
| π |
| 3 |
A、y=sin（
| ||||
B、y=sin（2x+
| ||||
C、y=sin（2x-
| ||||
D、y=sin（2x-
|
角α终边上有一点（-1，2），则下列各点中在角2α的终边上的点是（ ）
| A、（3，4） |
| B、（-3，-4） |
| C、（4，3） |
| D、（-4，-3） |
锐角△ABC中，三个内角分别为A，B，C，设m=sin A+sinB+sinC，n=cosA+cosB+cosC，则m与n的大小关系是（ ）
| A、m＞n | B、m＜n |
| C、m-n | D、以上都有可能 |
已知i是虚数单位，则
=（ ）
| i | ||
1+
|
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|