题目内容
定义在R上的奇函数f(x)满足:当x>0时,f(x)=2013x+log2013x,则方程f(x)=0的实数根的个数是( )
| A、1 | B、2 | C、3 | D、5 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:首先,根据奇函数的性质,得到f(0)=0,然后,当x>0时,在同一坐标系内画出函数y=-2013x y=log2013x,可以得到图象有一个交点,得到方程有一个实根,然后,根据对称性得到相应的方程的根的个数.
解答:
解:∵在R上的奇函数f(x),
∴f(0)=0,
∴x=0是方程f(x)=0的一个实根,
当x>0时,f(x)=2013x+log2013x=0,
∴-2013x=log2013x,
设函数y=-2013x y=log2013x,
在同一坐标系中作出它们的图象如下:
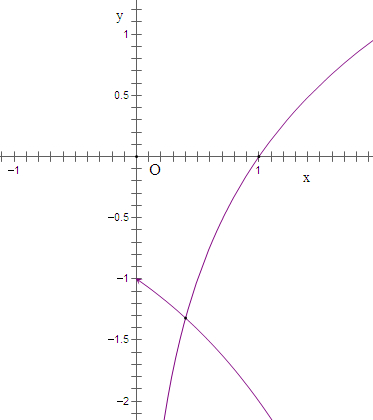
∴当x>0时,该方程有一个实根,
又∵函数为奇函数,
∴它们的图象关于坐标原点对称,
∴当x<0时,该方程也有一个实根,
总之,该方程有三个实根,
故选:C
∴f(0)=0,
∴x=0是方程f(x)=0的一个实根,
当x>0时,f(x)=2013x+log2013x=0,
∴-2013x=log2013x,
设函数y=-2013x y=log2013x,
在同一坐标系中作出它们的图象如下:

∴当x>0时,该方程有一个实根,
又∵函数为奇函数,
∴它们的图象关于坐标原点对称,
∴当x<0时,该方程也有一个实根,
总之,该方程有三个实根,
故选:C
点评:本题综合考查了函数为奇函数及其性质,属于中档题,掌握数形结合思想在求解问题中的灵活运用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
若将圆x2+y2=π2内的正弦曲线y=sinx与x轴围成的区域记为M,则在网内随机放一粒豆子,落入M的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点O,N在△ABC所在的平面内,且|
|=|
|=|
|,
+
+
=
,则点O,N依次是△ABC的( )
| OA |
| OB |
| OC |
| NA |
| NB |
| NC |
| 0 |
| A、外心,内心 |
| B、外心,重心 |
| C、重心,外心 |
| D、重心,内心 |
已知数列8,5,2,…,则-49可能是这个数列的第几项( )
| A、18 | B、19 | C、20 | D、21 |
执行如图所示的程序框图,若输入a1=1,k=4,则输出的S值为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知a=log
3,b=20.1,c=3-0.1,则a,b,c的大小关系是( )
| 1 |
| 2 |
| A、c<b<a |
| B、a<c<b |
| C、a<b<c |
| D、b<c<a |