题目内容
已知a,b,c∈R*,且a+2b+3c=6,
(1)求a2+2b2+3c2的最小值;
(2)求证:
+
+
≥
.
(1)求a2+2b2+3c2的最小值;
(2)求证:
| a2 |
| 1+a |
| 2b2 |
| 3+b |
| 3c2 |
| 5+c |
| 9 |
| 7 |
考点:二维形式的柯西不等式
专题:不等式的解法及应用
分析:(1)由条件利用柯西不等式可得a2+2b2+3c2 ≥
=
,从而求得a2+2b2+3c2取得最小值.
(2)根据
+
+
≥
,以及a+2b+3c=6,即可证得结论.
| (a+2b+3c)2 |
| 1+2+3 |
| 62 |
| 6 |
(2)根据
| a2 |
| 1+a |
| 2b2 |
| 3+b |
| 3c2 |
| 5+c |
| (a+2b+3c)2 |
| (a+1)+2(3+b)+3(5+c) |
解答:
解:(1)利用柯西不等式可得a2+2b2+3c2≥
=
=6,
当且仅当
=
=
,即a=b=c=1时,a2+2b2+3c2取得最小值为6.
(2)证明:
+
+
≥
=
=
=
(*),
当且仅当
=
=
,即
=
=
,即 a:b:c=1:3:5,
即a=
、b=
、c=
时,(*)式取到等号.
| (a+2b+3c)2 |
| 1+2+3 |
| 62 |
| 6 |
当且仅当
| a2 |
| 1 |
| 2b2 |
| 2 |
| 3c2 |
| 3 |
(2)证明:
| a2 |
| 1+a |
| 2b2 |
| 3+b |
| 3c2 |
| 5+c |
| (a+2b+3c)2 |
| (a+1)+2(3+b)+3(5+c) |
| 62 |
| 22+a+2b+3c |
| 36 |
| 22+6 |
| 9 |
| 7 |
当且仅当
| a2 | ||
|
| ||
| 2(3+b) |
| 3c2 | ||
|
| a |
| 1+a |
| b |
| 3+b |
| c |
| 5+c |
即a=
| 3 |
| 11 |
| 9 |
| 11 |
| 15 |
| 11 |
点评:本题主要考查柯西不等式的应用,注意式子的变形,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
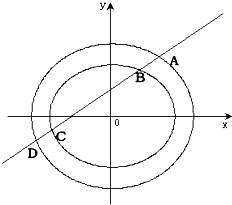 已知椭圆C1:
已知椭圆C1: