题目内容
已知各项均为正数的等比数列{an},首项a1=
,前n项和为Sn,且S3+a3,S5+a5,S4+a4成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn.
| 1 |
| 2 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{nan}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)利用等差数列和等比数列的通项公式、前n项和的意义即可得出;
(Ⅱ)由( I)知,nan=
,利用错位相减法求数列的前n项和即可得出.
(Ⅱ)由( I)知,nan=
| n |
| 2n |
解答:
解::(Ⅰ)设正项等比数列{an}(n∈N*)的公比为q(q>0),又a1=
,∴an=
•qn-1,
∵S3+a3、S5+a5、S4+a4成等差数列,
∴2(S5+a5)=(S3+a3)+(S4+a4),
即2(a1+a2+a3+a4+2a5)=(a1+a2+2a3)+(a1+a2+a3+2a4),
化简得4a5=a3,
∴4a1q4=a1q2,化为4q2=1,
解得q=±
∵q>0,
∴q=
,
∴an=
( II)由( I)知,nan=
,
则Tn=
+
+
+…+
,①
Tn=
+
+
+…+
+
,②…(8分)
①-②得:
Tn=
+
+…+
-
=
-
=1-
,
所以Tn=2-
.…(12分)
| 1 |
| 2 |
| 1 |
| 2 |
∵S3+a3、S5+a5、S4+a4成等差数列,
∴2(S5+a5)=(S3+a3)+(S4+a4),
即2(a1+a2+a3+a4+2a5)=(a1+a2+2a3)+(a1+a2+a3+2a4),
化简得4a5=a3,
∴4a1q4=a1q2,化为4q2=1,
解得q=±
| 1 |
| 2 |
∵q>0,
∴q=
| 1 |
| 2 |
∴an=
| 1 |
| 2n |
( II)由( I)知,nan=
| n |
| 2n |
则Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n-1 |
| 2n |
| n |
| 2n+1 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
| n+2 |
| 2n+1 |
所以Tn=2-
| n+2 |
| 2n |
点评:本题考查了等差数列和等比数列的通项公式及前n项和公式、“错位相减法”等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
已知
+
+
=
,|
|=2,|
|=3,|
|=
,则向量
与
的夹角为( )
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| 7 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |
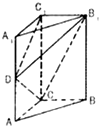 如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.
如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.