题目内容
函数y=x2（1-5x）（0＜x＜
）的最大值是 ．
| 1 |
| 5 |
考点：基本不等式
专题：不等式的解法及应用
分析：由于0＜x＜
，可得1-5x＞0，变形利用基本不等式可得y=x2（1-5x）=
•x•x•(
-2x)≤
(
)3即可得出．
| 1 |
| 5 |
| 5 |
| 2 |
| 2 |
| 5 |
| 5 |
| 2 |
x+x+
| ||
| 3 |
解答：
解：∵0＜x＜
，∴1-5x＞0，
∴函数y=x2（1-5x）=
•x•x•(
-2x)≤
(
)3=
，当且仅当x=
时取等号．
故答案为：
．
| 1 |
| 5 |
∴函数y=x2（1-5x）=
| 5 |
| 2 |
| 2 |
| 5 |
| 5 |
| 2 |
x+x+
| ||
| 3 |
| 4 |
| 675 |
| 2 |
| 15 |
故答案为：
| 4 |
| 675 |
点评：本题考查了变形利用基本不等式，属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
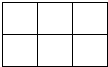某农场有如图所示的2行3列共六块土地，现有萝卜、玉米、油菜三类蔬菜可种．要求每块土地种一类蔬菜，每类蔬菜种两块土地，每行的蔬菜种类各不相同，则恰有一类蔬菜种在同列的种植方法数为