题目内容
要得到函数y=cos2x的图象,只需要把函数y=sin(2x+
)的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:已知函数y=sin(2x+
) 即y=cos(2x-
),再根据函数y=Acos(ωx+φ)的图象变换规律,可得结论.
| π |
| 6 |
| π |
| 3 |
解答:
解:把函数y=sin(2x+
)=cos(
-2x)=cos(2x-
)的图象向左平移
个单位长度,可得函数y=cos[2(x+
)-
]=cos2x的图象,
故选:C.
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
故选:C.
点评:本题主要考查诱导公式的应用,函数y=Acos(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题

练习册系列答案
相关题目
已知sin(θ+π)<0,cos(θ-π)>0,则θ是第( )象限角.
| A、一 | B、二 | C、三 | D、四 |
已知集合A={x|x2-2x>0},B={x|-2<x<
},则( )
| 6 |
| A、A∩B=∅ | B、A∪B=R |
| C、B⊆A | D、A⊆B |
在如图程序框图的结构中最突出的逻辑结构及输出的i的值是( )
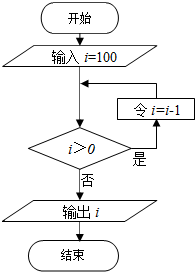

| A、当型循环结构,-1 |
| B、直到型循环结构,-1 |
| C、当型循环结构,0 |
| D、直到型循环结构,0 |
已知函数f(x)是定义在R上的奇函数,f(1)=0,当x>0时,有
>0成立,则不等式f(x)>0的解集是( )
| xf′(x)-f(x) |
| x2 |
| A、(-1,0)∪(1,+∞) |
| B、(-1,0) |
| C、(1,+∞) |
| D、(-∞,-1)∪(1,+∞) |
观察:52-1=24,72-1=48,112-1=120,132-1=168,…所得的结果都是24的倍数,由此推测可有( )
| A、其中包含等式:152-1=224 |
| B、一般式是:(2n+3)2-1=4(n+1)(n+2) |
| C、其中包含等式1012-1=10200 |
| D、24的倍数加1必是某一质数的完全平方 |
已经集合M={-1,0,1,2,3,4,5},N={x|x≤1或x≥4},则M∩N=( )
| A、{-1,0,1,4,5} |
| B、{1,2,3,4} |
| C、{-1,0,5} |
| D、{-1,0,1,5} |
已知定点M(x0,y0)在直线l:f(x,y)=0外,则方程f(x,y)=f(x0,y0)表示( )
| A、与l重合的直线 |
| B、与l平行的直线 |
| C、与l垂直的直线 |
| D、点M(x0,y0) |