题目内容
已知集合M={0,1,2,3},N={x|x2-3x<0},则M∩N=( )
| A、{0} |
| B、{x|x<0} |
| C、{x|0<x<3} |
| D、{1,2} |
考点:交集及其运算
专题:计算题,集合
分析:求出N中不等式的解集确定出N,再找出两集合的交集即可.
解答:
解:由N中的不等式变形得:x(x-3)<0,
解得:0<x<3,即N=(0,3),
∵M={0,1,2,3},
∴M∩N=[1,2}.
故选:D.
解得:0<x<3,即N=(0,3),
∵M={0,1,2,3},
∴M∩N=[1,2}.
故选:D.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
设函数f(x)=ex(sinx-cosx)(0≤x≤40π),则函数f(x)各极小值点之和为( )
| A、380π | B、800π |
| C、420π | D、820π |
扇形的面积为6cm2,半径为2cm,则扇形的圆心角是( )
| A、3 | ||
| B、3π | ||
C、
| ||
D、
|
交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,22,26,44,则这四个社区驾驶员的总人数N为( )
| A、104 | B、808 |
| C、832 | D、2014 |
在如图程序框图的结构中最突出的逻辑结构及输出的i的值是( )
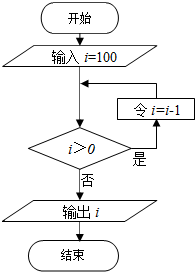

| A、当型循环结构,-1 |
| B、直到型循环结构,-1 |
| C、当型循环结构,0 |
| D、直到型循环结构,0 |
已知f1(x)=sinx+cosx,fn+1(x)是fn (x)的导函数,即f2(x)=f′1(x),f3(x)=f′2(x),…,fn+1(x)=f′n(x),n∈N*,则f2012(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
观察:52-1=24,72-1=48,112-1=120,132-1=168,…所得的结果都是24的倍数,由此推测可有( )
| A、其中包含等式:152-1=224 |
| B、一般式是:(2n+3)2-1=4(n+1)(n+2) |
| C、其中包含等式1012-1=10200 |
| D、24的倍数加1必是某一质数的完全平方 |
已知{an}是公差不为0的等差数列,且an≥0;又定义bn=
+
(1≤n≤2003 ),则{bn}的最大项是( )
| an |
| a2004-n |
| A、b1001 |
| B、b1002 |
| C、b2003 |
| D、不能确定的 |