题目内容
2.若实数x,y满足$\left\{\begin{array}{l}{x+y-1≥0}\\{y-x-1≤0}\\{x≤1}\end{array}\right.$,则z=2x+3y的最大值为8.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y-1≥0}\\{y-x-1≤0}\\{x≤1}\end{array}\right.$作出可行域如图,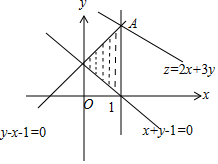
联立$\left\{\begin{array}{l}{x=1}\\{y-x-1=0}\end{array}\right.$,解得A(1,2),
化目标函数z=2x+3y为$y=-\frac{2}{3}x+\frac{2}{3}z$,
由图可知,当直线$y=-\frac{2}{3}x+\frac{2}{3}z$过A时,直线在y轴上的截距最大,z有最大值为8.
故答案为:8.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
12.有一个几何体的三视图如图所示,这个几何体应是一个( )
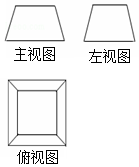

| A. | 棱台 | B. | 棱锥 | C. | 棱柱 | D. | 正四面体 |
10.已知直线m,n是平面α,β外的两条直线,且m∥α,n⊥β,α⊥β,则( )
| A. | m∥n | B. | m⊥n | C. | n∥α | D. | n⊥α |
17.一片森林原有面积为a,现计划每年采伐一些树木,且每年采伐的森林面积占上一年底森林面积的百分比为q,即第x(x∈N)年底的剩余森林面积为y=a(1-q)x,x与y的部分对应值如表:
(1)求原有森林面积a和每年采伐森林面积的百分比q;
(2)问经过多少年后,剩余的森林面积开始小于原来的$\frac{1}{10}$.
(注:lg2≈0.301,lg3≈0.477)
| x | 0 | 1 | 2 |
| y | a | $\frac{20}{3}$ | $\frac{40}{9}$ |
(2)问经过多少年后,剩余的森林面积开始小于原来的$\frac{1}{10}$.
(注:lg2≈0.301,lg3≈0.477)
14.已知实数x,y满足$\left\{\begin{array}{l}x+y-4≤0\\ x-y≤0\\ x≥1\end{array}\right.$,则z=2x+3y的最大值为( )
| A. | 5 | B. | 8 | C. | 10 | D. | 11 |
11.已知P是直线3x+4y+8=0上的动点,PA,PB是圆x2+y2-2x-2y+1=0的切线,A,B是切点,C是圆心,那么四边形PACB面积的最小值是( )
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | 不存在 |
1.命题p:?x0≥2,x02-2x0-2>0的否定是( )
| A. | ?x0≥2,x02-2x0-2<0 | B. | ?x0<2,x02-2x0-2<0 | ||
| C. | ?x<2,x2-2x-2≤0 | D. | ?x≥2,x2-2x-2≤0 |
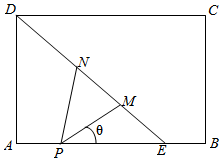 如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN=$\frac{π}{4}$,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在△ADE区域内参观,在AE上点P处安装一可旋转的监控摄像头,∠MPN为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方,经测量得知:AD=6米,AE=6米,AP=2米,∠MPN=$\frac{π}{4}$,记∠EPM=θ(弧度),监控摄像头的可视区域△PMN的面积为S平方米.