题目内容
14.已知实数x,y满足$\left\{\begin{array}{l}x+y-4≤0\\ x-y≤0\\ x≥1\end{array}\right.$,则z=2x+3y的最大值为( )| A. | 5 | B. | 8 | C. | 10 | D. | 11 |
分析 作出不等式组对应的平面区域,z=2x+3y,目标函数的几何意义,通过数形结合即可的得到结论.
解答 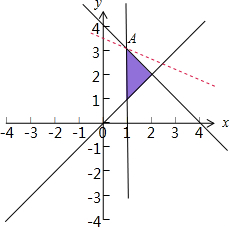 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
z=2x+3y,得y=$-\frac{2}{3}$x+$\frac{1}{3}z$,
平移直线y=$-\frac{2}{3}$x+$\frac{1}{3}z$,由图象可知当直线y=$-\frac{2}{3}$x+$\frac{1}{3}z$经过点A时,
直线y=$-\frac{2}{3}$x+$\frac{1}{3}z$的截距最大,由$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$,解得A(1,3),
此时z最大,zmax=2×1+3×3=11.
故选:D.
点评 本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
4.一个几何体的三视图如图所示,则该几何体的表面积为( )
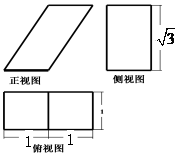

| A. | 2+4$\sqrt{3}$ | B. | 4+4$\sqrt{3}$ | C. | 8+2$\sqrt{3}$ | D. | 6+2$\sqrt{3}$ |
5.如图,△A'O'B'为水平放置的△AOB的直观图,且O'A'=2,O'B'=3,则△AOB的周长为( )


| A. | 12 | B. | 10 | C. | 8 | D. | 7 |
19.某学校有教职工150人,其中高级职称45人,中级职称90人,一般职员15人.现用分层抽样的方法抽取一个容量为10的样本,则各职称抽取的人数分别为( )
| A. | 5,15,5 | B. | 3,6,1 | C. | 3,10,17 | D. | 5,9,16 |
3.在△ABC中,内角A,B,C的对边分别是a,b,c,若a2=b2+c2+$\sqrt{3}$bc,则角A是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
13.点A(2,0)到直线l:y=x+2的距离为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |