题目内容
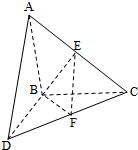 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.(Ⅰ)求证:EF⊥BC;
(Ⅱ)求二面角E-BF-C的正弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的性质,二面角的平面角及求法
专题:空间位置关系与距离
分析:(Ⅰ)以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,得到E、F、B、C点的坐标,易求得此
•
=0,所以EF⊥BC;
(Ⅱ)设平面BFC的一个法向量
=(0,0,1),平面BEF的法向量
=(x,y,z),依题意,可求得一个
=(1,-
,1),设二面角E-BF-C的大小为θ,可求得sinθ的值.
| EF |
| BC |
(Ⅱ)设平面BFC的一个法向量
| n1 |
| n2 |
| n2 |
| 3 |
解答:
 (Ⅰ)证明:由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,易得B(0,0,0),A(0,-1,
(Ⅰ)证明:由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,易得B(0,0,0),A(0,-1,
),D(
,-1,0),C(0,2,0),因而E(0,
,
),F(
,
,0),所以
=(
,0,-
),
=(0,2,0),因此
•
=0,所以EF⊥BC.
(Ⅱ)解:在图中,设平面BFC的一个法向量
=(0,0,1),平面BEF的法向量
=(x,y,z),又
=(
,
,0),
=(0,
,
),
由
得其中一个
=(1,-
,1),
设二面角E-BF-C的大小为θ,由题意知θ为锐角,则
cosθ=|cos<
,
>|=|
|=
,
因此sinθ=
=
,即所求二面角正弦值为
.
 (Ⅰ)证明:由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,易得B(0,0,0),A(0,-1,
(Ⅰ)证明:由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系,易得B(0,0,0),A(0,-1,| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| EF |
| ||
| 2 |
| ||
| 2 |
| BC |
| EF |
| BC |
(Ⅱ)解:在图中,设平面BFC的一个法向量
| n1 |
| n2 |
| BF |
| ||
| 2 |
| 1 |
| 2 |
| BE |
| 1 |
| 2 |
| ||
| 2 |
由
|
| n2 |
| 3 |
设二面角E-BF-C的大小为θ,由题意知θ为锐角,则
cosθ=|cos<
| n1 |
| n2 |
| ||||
|
|
| 1 | ||
|
因此sinθ=
| 2 | ||
|
2
| ||
| 5 |
2
| ||
| 5 |
点评:本题主要考查空间点、线、面位置关系,二面角等基础知识,同时考查空间想象能力,空间向量的坐标运算,推理论证能力和运算求解能力.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知函数f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4 |
| 2015 |
| 2014 |
| 2015 |
| A、1007 | B、2014 |
| C、2015 | D、4028 |
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.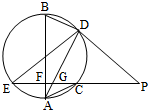 如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.