题目内容
7．设$\overrightarrow a=（2，-1），向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=（-1，3），则$\overrightarrow b$等于（ ）| A． | （-5，5） | B． | （5，-5） | C． | （-3，3） | D． | （3，-3） |
分析 设$\overrightarrow{b}$=（x，y），由$\overrightarrow a=（2，-1），向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=（-1，3），利用平面向量坐标运算法则能求出$\overrightarrow{b}$．
解答 解：设$\overrightarrow{b}$=（x，y），
∵$\overrightarrow a=（2，-1），向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=（-1，3），
∴（4-x，-2-y）=（-1，3），
∴$\left\{\begin{array}{l}{4-x=-1}\\{-2-y=3}\end{array}\right.$，解得x=5，y=-5，
∴$\overrightarrow{b}$=（5，-5）．
故选：B．
点评 本题考查向量的求法，是基础题，解题时要认真审题，注意平面向量坐标运算法则的合理运用．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
17．若椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$过抛物线y2=8x的焦点，且与双曲线${x^2}-\frac{y^2}{2}=1$有相同的焦点，则该椭圆的方程是（ ）
| A． | $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ | B． | $\frac{x^2}{4}+{y^2}=1$ | C． | ${x^2}+\frac{y^2}{4}=1$ | D． | $\frac{{x}^{2}}{2}$+$\frac{y^2}{4}$=1 |
18．若函数f（x）=mx2+4mx+3＞0在R上恒成立，则实数m的取值范围是（ ）
| A． | [0，$\frac{2}{3}$） | B． | [0，$\frac{3}{4}$） | C． | （$\frac{3}{4}$，+∞） | D． | （0，$\frac{2}{3}$） |
15．抛物线y=-$\frac{1}{8}{x}^{2}$的准线方程是（ ）
| A． | x=$\frac{1}{32}$ | B． | x=$\frac{1}{2}$ | C． | y=2 | D． | y=4 |
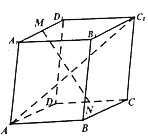已知平行六面体ABCD-A1B1C1D1，设A1D1中点为M，CD的中点为N，若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1，则|AC1|=$\sqrt{6}$，若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$，则x+y+z=0．
12．若tan（α-β）=$\frac{1}{2}$，tan（α+β）=$\frac{1}{3}$，则tan2β等于（ ）
| A． | $\frac{1}{7}$ | B． | $\frac{4}{3}$ | C． | -$\frac{1}{7}$ | D． | -$\frac{4}{3}$ |
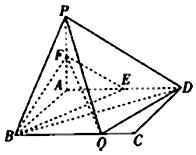如图，在矩形ABCD中，AB=1，AD=a，PA⊥平面ABCD，且PA=1，E，F分别为AD，PA中点，在BC上有且只有一个点Q，使得PQ⊥QD．