题目内容
3.已知函数f(x)=2sin(2ωx+$\frac{π}{3}$)(ω>0),最小正周期为π(1)求ω的值;
(2)将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度,再将所得图象各点的横坐标缩小为原来的$\frac{1}{2}$(纵坐标不变),得到函数g(x)的图象,求g(x)的单调区间.
分析 (1)利用正弦函数的周期性,求得ω的值.
(2)利用y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再根据正弦函数的单调性,求得g(x)的单调区间.
解答 解:(1)由于函数f(x)=2sin(2ωx+$\frac{π}{3}$)(ω>0)的最小正周期为$\frac{2π}{2ω}$=π,∴ω=1.
(2)将函数f(x)=2sin(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位长度,
可得y=2sin[2(x+$\frac{π}{6}$)+$\frac{π}{3}$]=2sin(2x+$\frac{2π}{3}$)的图象,
再将所得图象各点的横坐标缩小为原来的$\frac{1}{2}$(纵坐标不变),
得到函数g(x)=2sin(4x+$\frac{2π}{3}$)的图象.
令2kπ-$\frac{π}{2}$≤4x+$\frac{2π}{3}$≤2kπ+$\frac{π}{2}$,求得$\frac{kπ}{2}$-$\frac{7π}{24}$≤x≤$\frac{kπ}{2}$-$\frac{π}{24}$,
故函数g(x)的增区间为[$\frac{kπ}{2}$-$\frac{7π}{24}$,$\frac{kπ}{2}$-$\frac{π}{24}$],k∈Z.
令2kπ+$\frac{π}{2}$≤4x+$\frac{2π}{3}$≤2kπ+$\frac{3π}{2}$,求得$\frac{kπ}{2}$-$\frac{π}{24}$≤x≤$\frac{kπ}{2}$+$\frac{5π}{24}$,
故函数g(x)的增区间为[$\frac{kπ}{2}$-$\frac{π}{24}$,$\frac{kπ}{2}$+$\frac{5π}{24}$],k∈Z.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性、单调性,属于基础题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
| A. | f(-1)<f(2)<f(3) | B. | f(2)<f(3)<f(-4) | C. | f(-2)<f(0)<f($\frac{1}{2}$) | D. | f(5)<f(-3)<f(-1) |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
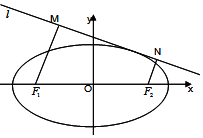 已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.
已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.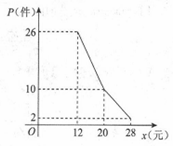 某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.