题目内容
19.设函数f(x)在(-∞,+∞)上有意义,对于给定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}f(x),f(x)<k\\ k,f(x)≥k\end{array}\right.$,取k=3,f(x)=($\frac{k}{2}$)|x|,则fk(x)=$\frac{k}{2}$的零点有( )| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
分析 先根据题中所给函数定义,求出函数函数fK(x)的解析式,从而得到一个分段函数,然后再利用指数函数的性质求出所求即可.
解答 解:函数fk(x)=$\left\{\begin{array}{l}{{3}^{x},0<x<1}\\{{3}^{-x},-1<x<0}\\{3,x≥1或x≤-1}\end{array}\right.$的图象如图所示:
则fk(x)=$\frac{k}{2}=\frac{3}{2}$的零点就是fk(x)与y=$\frac{3}{2}$的交点,故交点有两个,即零点两个.
故选:C
点评 本题为新定义问题,正确理解新定义的含义是解决此类问题的关键.本题还考查含有绝对值的函数的性质问题

练习册系列答案
相关题目
9.已知实数x,y满足不等式组$\left\{\begin{array}{l}{2x+y≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,则$\frac{y+1}{x+1}$的最大值为( )
| A. | 3 | B. | 5 | C. | 4 | D. | 6 |
7.设$\overrightarrow a=(2,-1),向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=(-1,3),则$\overrightarrow b$等于( )
| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
15.已知函数f(x)是定义在R上的偶函数,在(-∞,0]上有单调性,且f(-2)<f(1),则下列不等式成立的是( )
| A. | f(-1)<f(2)<f(3) | B. | f(2)<f(3)<f(-4) | C. | f(-2)<f(0)<f($\frac{1}{2}$) | D. | f(5)<f(-3)<f(-1) |
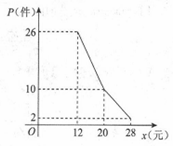 某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.