题目内容
18.若函数f(x)=mx2+4mx+3>0在R上恒成立,则实数m的取值范围是( )| A. | [0,$\frac{2}{3}$) | B. | [0,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,+∞) | D. | (0,$\frac{2}{3}$) |
分析 对m讨论,分m=0,显然成立;m<0,不恒成立;m>0且△=16m2-12m<0,解出m的范围,最后合并即可得到所求范围.
解答 解:mx2+4mx+3>0在R上恒成立,
当m=0时,3>0恒成立;
当m<0时,不等式不恒成立;
当m>0且△=16m2-12m<0,
即为m>0且0<m<$\frac{3}{4}$,
即有0<m<$\frac{3}{4}$,
综上可得实数m的取值范围是0≤m<$\frac{3}{4}$.
故选:B.
点评 本题考查不等式恒成立问题的解法,注意运用二次函数的图象和性质,以及分类讨论思想方法,属于中档题和易错题.

练习册系列答案
相关题目
8.设曲线x=$\sqrt{2y-{y}^{2}}$上的点到直线x-y-2=0的距离的最大值为a,最小值为b,则a-b的值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$+1 | D. | 2 |
9.已知实数x,y满足不等式组$\left\{\begin{array}{l}{2x+y≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,则$\frac{y+1}{x+1}$的最大值为( )
| A. | 3 | B. | 5 | C. | 4 | D. | 6 |
7.设$\overrightarrow a=(2,-1),向量\overrightarrow b满足2\overrightarrow a-\overrightarrow b$=(-1,3),则$\overrightarrow b$等于( )
| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
15.已知函数f(x)是定义在R上的偶函数,在(-∞,0]上有单调性,且f(-2)<f(1),则下列不等式成立的是( )
| A. | f(-1)<f(2)<f(3) | B. | f(2)<f(3)<f(-4) | C. | f(-2)<f(0)<f($\frac{1}{2}$) | D. | f(5)<f(-3)<f(-1) |
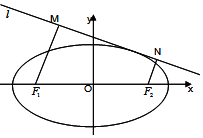 已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.
已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.