题目内容
4.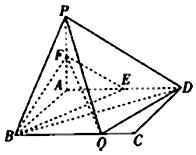 如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.
如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.(1)求证:平面BEF∥平面PDQ;
(2)求二面角E-BF-Q的余弦值.
分析 (1)以A点为原点,分别以$\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AP}$的方向为x轴,y轴,z轴的正方向,建立空间直角坐标系Axyz,求出相关点的坐标,设Q(1,x,0),则$\overrightarrow{PQ}=({1,x,-1})$,利用PQ⊥QD,求出x=1.推出BE∥DQ,推出EF∥PD,EF∥平面PDQ,然后证明平面BEF∥平面PDQ.
(2)求出 平面BFQ是一个法向量,平面BEF的一个法向量,利用空间向量的数量积求解即可.
解答 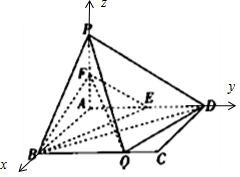 解:(1)以A点为原点,分别以$\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AP}$的方向为x轴,y轴,z轴的正方向,
解:(1)以A点为原点,分别以$\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AP}$的方向为x轴,y轴,z轴的正方向,
建立空间直角坐标系Axyz,
则A(0,0,0),B(1,0,0),D(0,a,0),P(0,0,1),
设Q(1,x,0),则$\overrightarrow{PQ}=({1,x,-1})$,$\overrightarrow{DQ}=({-1,a-x,0})$,…(2分)
若PQ⊥QD,则$\overrightarrow{PQ}•\overrightarrow{QD}=-1+x({a-x})=0$,
即x2-ax+1=0,△=a2-4,
∴△=0,a=2,x=1.…(4分)
∴$Q({1,1,0}),\overrightarrow{QD}({-1,1,0})$,
又E是AD中点,∴E(0,1,0),$\overrightarrow{BE}=({-1,1,0})$,∴$\overrightarrow{QD}=\overrightarrow{BE}$,∴BE∥DQ,
又BE?平面PDQ,DQ?平面PDQ,∴BE∥平面PDQ,
又F是PA中点,∴EF∥PD,
∵EF?平面PDQ,PD?平面PDQ,∴EF∥平面PDQ,
∵BE∩EF=E,BE,EF?平面PDQ,∴平面BEF∥平面PDQ.…(6分)
(2)设平面BFQ是一个法向量$\overrightarrow m=({x,y,z})$,则$\overrightarrow m•\overrightarrow{BF}=\overrightarrow m•\overrightarrow{BQ}=0$,
由(1)知$\overrightarrow{BF}=({-1,0,\frac{1}{2}})$,$\overrightarrow{BQ}=({0,1,0})$,
∴$-x+\frac{1}{2}z=y=0$,取z=2,得$\overrightarrow m=({1,0,2})$,
同样求平面BEF的一个法向量$\overrightarrow n=({1,1,2})$,$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{{\sqrt{30}}}{6}$,
∴二面角E-BF-Q的余弦值为$\frac{{\sqrt{30}}}{6}$.…(12分)
点评 本题考查直线与平面平行,平面与平面平行的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.

| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
| A. | f(-1)<f(2)<f(3) | B. | f(2)<f(3)<f(-4) | C. | f(-2)<f(0)<f($\frac{1}{2}$) | D. | f(5)<f(-3)<f(-1) |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
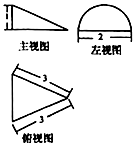
| A. | $\frac{\sqrt{2}}{3}$π | B. | 2$\sqrt{2}$+2π | C. | $\frac{2\sqrt{2}}{3}$π | D. | 2$\sqrt{2}$+$\frac{3}{2}$π |
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |