题目内容
化简式子:
.
lg5•lg8000+(lg2
| ||||
lg600-
|
考点:对数的运算性质
专题:函数的性质及应用
分析:直接根据对数的运算性质进行计算.
解答:
解:
=
=
=
=
.
lg5•lg8000+(lg2
| ||||
lg600-
|
=
lg5(lg8+3)+(
| ||||
2+lg6-
|
=
| (1-lg2)•(3lg2+3)+3(lg2)2 |
| 2+lg6-lg0.1-lg0.36 |
=
| 3lg2+3-3(lg2)2-3lg2+3(lg2)2 | ||
2+lg6-(-1)-
|
=
| 3 |
| 4 |
点评:本题重考查了对数的运算性质,注意对数的加减法运算和实数的运算性质的区别.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
数列{an}中,a1=2,an+1=an+log2
,则a8=( )
| n+1 |
| n |
| A、3 | B、4 | C、5 | D、6 |
化简:(sinα+cosα)2=( )
| A、1+sin2α |
| B、1-sinα |
| C、1-sin2α |
| D、1+sinα |
已知cosα=
,α∈(370°,520°),则α等于( )
| 1 |
| 2 |
| A、390° | B、420° |
| C、450° | D、480° |
已知函数f(x)是R上的增函数,A(0,-1),B(3,1)是其图象上的两点,那么f(x+1)<1的解集的补集是( )
| A、(-1,2) |
| B、(1,4) |
| C、[2,+∞) |
| D、[4,+∞) |
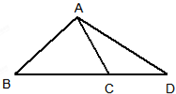 如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.
如图,在△ABC中,内角A,B,C的对边分别是a,b,c,且bsinA=acosB,D是BC延长线上的一点,AC=5,AD=7,CD=3.